Ein Techniker wählt 10 Teile aus, die den erwarteten Bereich der Prozessstreuung darstellen. Drei Prüfer messen die 10 Teile in zufälliger Reihenfolge, jedes Teil jeweils dreimal.
Der Ingenieur führt eine gekreuzte MPA-Studie durch, um die Variabilität der Messungen zu bewerten, die vom Messsystem stammen können.
- Öffnen Sie die Beispieldaten Messsystemdaten.MWX.
- Wählen Sie aus.
- Geben Sie im Feld Teile die Spalte Teil ein.
- Geben Sie im Feld Prüfer die Spalte Prüfer ein.
- Geben Sie im Feld Messwerte die Spalte Messung ein.
- Wählen Sie unter Analysemethode die Option ANOVA aus.
- Klicken Sie in den einzelnen Dialogfeldern auf OK.
Interpretieren der Ergebnisse
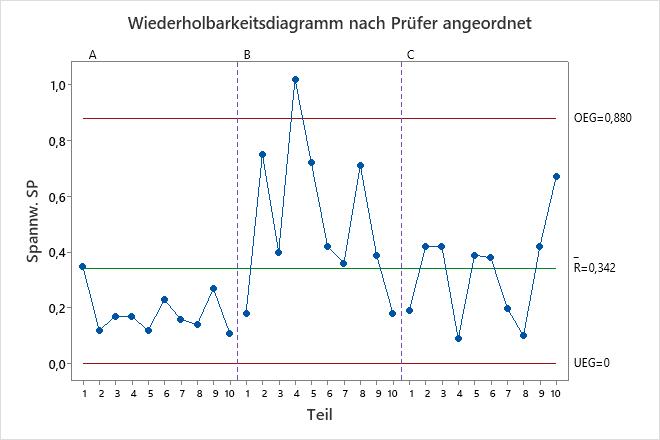
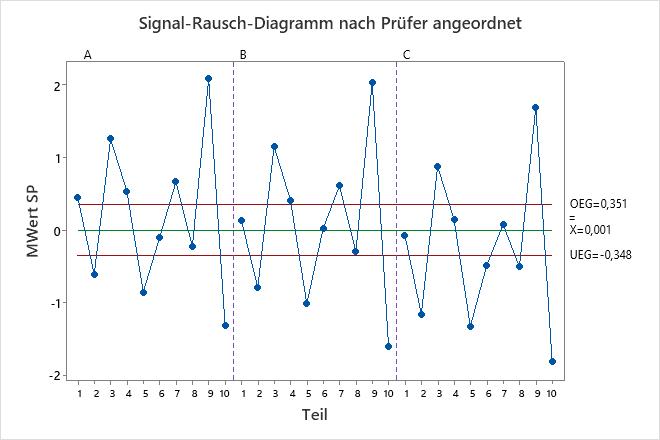
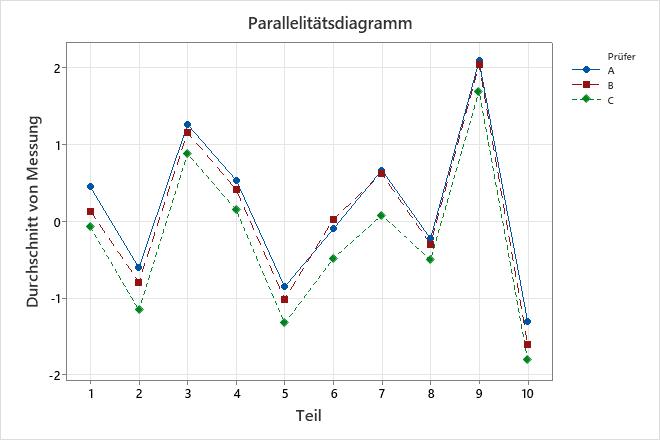
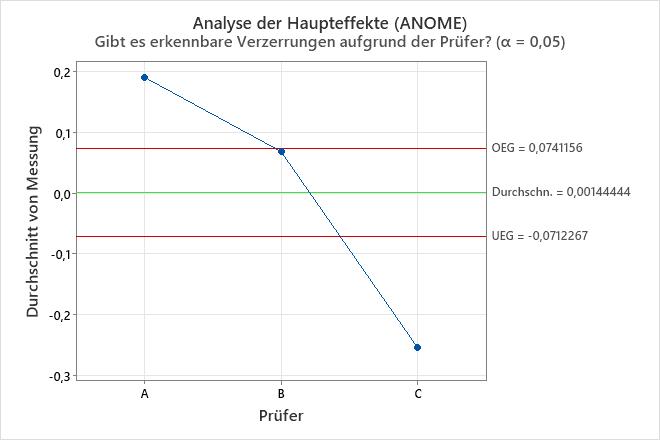
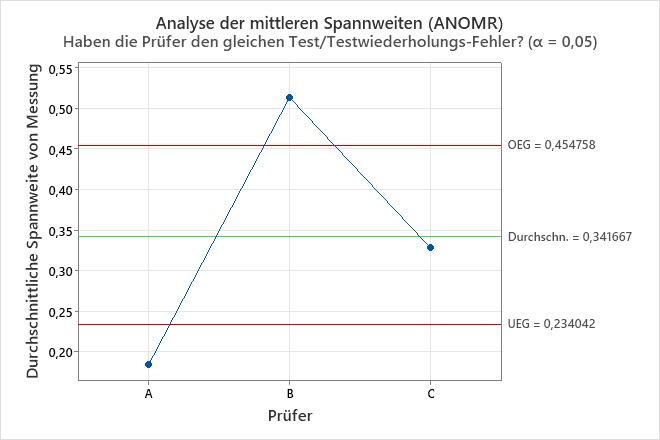
Die Tabelle der Varianzkomponenten und die Diagramme zeigen Möglichkeiten zur Verbesserung des Messsystems. Das Wiederholbarkeitsdiagramm weist z. B. einen Punkt außerhalb der Eingriffsgrenzen auf. Untersuchen Sie diesen Punkt, um potenzielle Messprobleme zu identifizieren. Die Punkte außerhalb der Entscheidungsgrenzen im Diagramm "Analyse der Haupteffekte" und im Diagramm "Analyse der mittleren Bereiche" zeigen, dass die Operatoren die Teile unterschiedlich messen. Untersuchen Sie, wie die Prüfer die Teile messen, um das Messsystem zu verbessern. Das Parallelitätsdiagramm gibt Aufschluss über die Unterschiede zwischen den Operatoren. In diesen Daten zeigt das Parallelitätsdiagramm, dass Operator C für jedes Teil den geringsten Durchschnittswert aufweist.
Die Tabelle "Klassifizierungsrichtlinien" gibt die Wahrscheinlichkeit einer Warnung für ein X-quer-Diagramm an, das innerhalb von zehn Untergruppen für Test 1 oder für Tests 1, 5, 6 und 8 außer Kontrolle geraten ist. Erstklassige und zweitklassige Messsysteme sind in der Regel ausreichend für Prozessverbesserungsaktivitäten mit einem X-Balken-Diagramm, das Test 1 verwendet. Drittklassige Messsysteme sind in der Regel für Prozessverbesserungsaktivitäten mit einem X-Balken-Diagramm ausreichend, das die Regeln 1, 5, 6 und 8 verwendet. In diesen Daten zeigen die MPA-Statistiken, dass das Messsystem erstklassig ist. Auch wenn das Messsystem Verbesserungsmöglichkeiten aufzeigt, ist das System für viele Aktivitäten zur Prozessverbesserung ausreichend.
In der Tabelle "Effektive Auflösung der Messwerte" wird die Genauigkeit der Messungen mit dem wahrscheinlichen Fehler des Messsystems verglichen. In diesen Daten enthalten die Messungen eine Hundertstelstelle, aber der wahrscheinliche Fehler liegt bei mehr als einem Zehntel. Die Ergebnisse empfehlen, dass die Messungen an der Zehntelstelle statt an der Hundertstelstelle erfolgen. Der Ingenieur plant, die Messungen zu runden und sich dann die neuen EMP-Statistiken anzusehen, um zu überprüfen, ob die Schlussfolgerungen identisch sind.
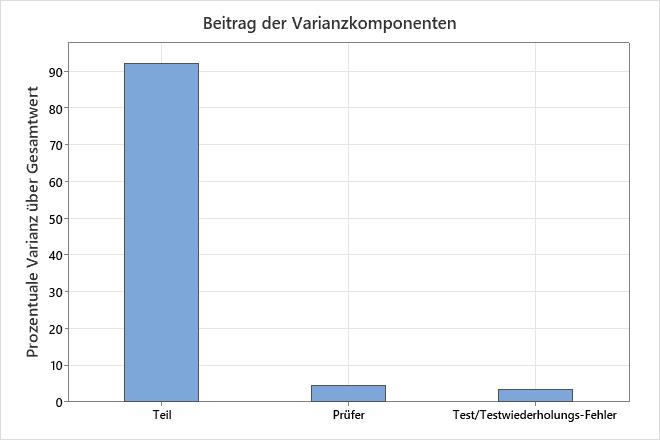
Varianzkomponenten
| Quelle | Varianz | %Gesamt | StdAbw |
|---|---|---|---|
| Test/Testwiederholungs-Fehler (Wiederholbarkeit) | 0,03997 | 3,394 | 0,19993 |
| Prüfer (Reproduzierbarkeit) | 0,05146 | 4,368 | 0,22684 |
| Teil (Produktstreuung) | 1,08645 | 92,238 | 1,04233 |
| Gesamt | 1,17788 | 100,000 | 1,08530 |
MPA-Statistiken
| Statistik | Wert | Klassifikation |
|---|---|---|
| Test/Testwiederholungs-Fehler | 0,1999 | |
| Freiheitsgrade | 78,0000 | |
| Wahrscheinlicher Fehler | 0,1349 | |
| Intraklassen-Korrelation (keine Verzerrung) | 0,9645 | Erste Klasse |
| Intraklassen-Korrelation (mit Verzerrung) | 0,9224 | Erste Klasse |
| Auswirkung der Verzerrung | 0,0421 |
Klassifikationsrichtlinien
| Klassifikation | Intraklassen-Korrelation | Dämpfung der Prozesssignale | Warnwahrscheinlichkeit, Test 1* |
|---|---|---|---|
| Erste Klasse | 0,80 - 1,00 | Weniger als 11% | 0,99 - 1,00 |
| Zweite Klasse | 0,50 - 0,80 | 11 - 29% | 0,88 - 0,99 |
| Dritte Klasse | 0,20 - 0,50 | 29 - 55% | 0,40 - 0,88 |
| Vierte Klasse | 0,00 - 0,20 | Mehr als 55% | 0,03 - 0,40 |
| Klassifikation | Warnwahrscheinlichkeit, Tests* |
|---|---|
| Erste Klasse | 1,00 |
| Zweite Klasse | 1,00 |
| Dritte Klasse | 0,92 - 1,00 |
| Vierte Klasse | 0,08 - 0,92 |
Effektive Auflösung der Messwerte
| Quelle | Wert |
|---|---|
| Wahrscheinlicher Fehler (WF) | 0,134853 |
| Untergrenze des Inkrements (0,1 * WF) | 0,013485 |
| Kleinstes effektives Inkrement (0,22 * WF) | 0,029668 |
| Aktuelles Messinkrement | 0,010000 |
| Größtes effektives Inkrement (2,2 * WF) | 0,296676 |
