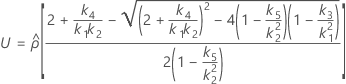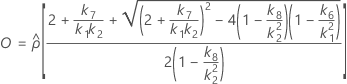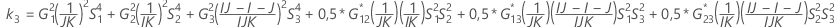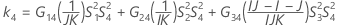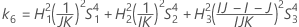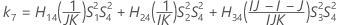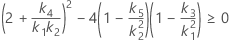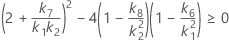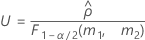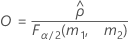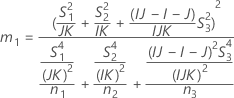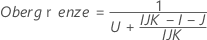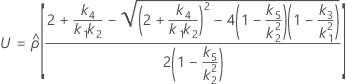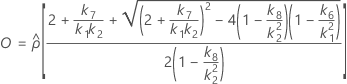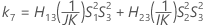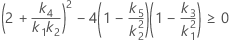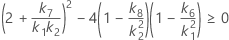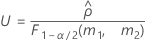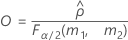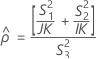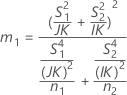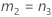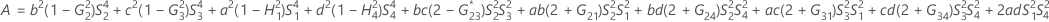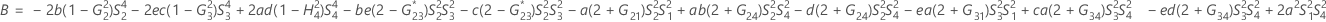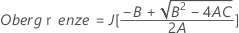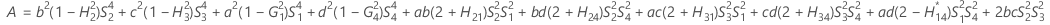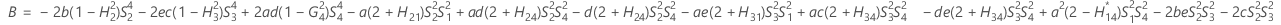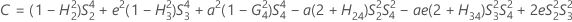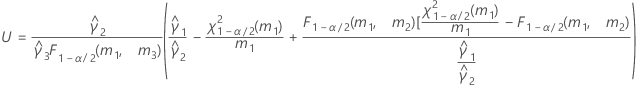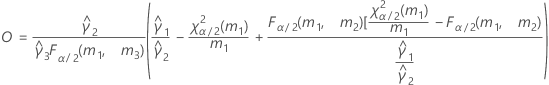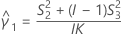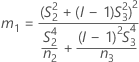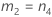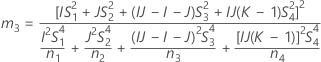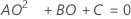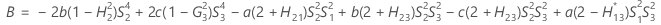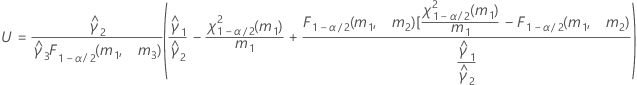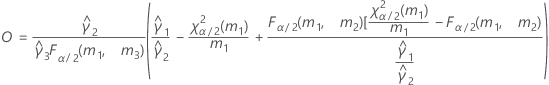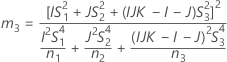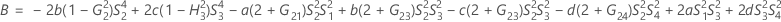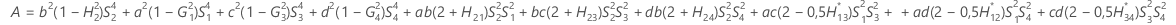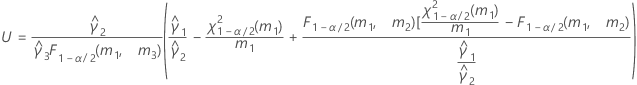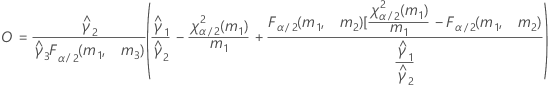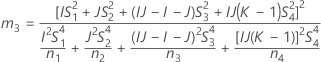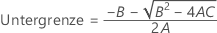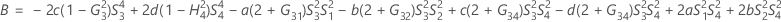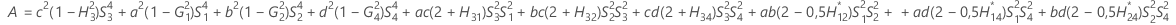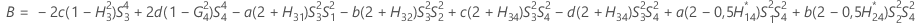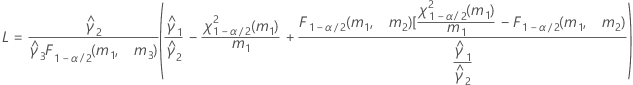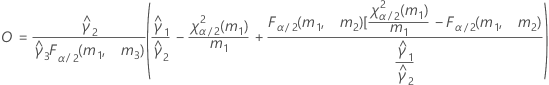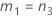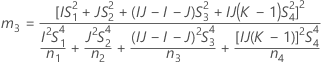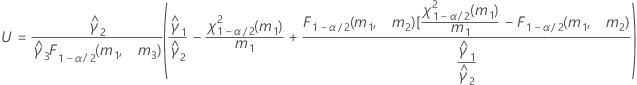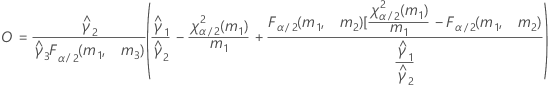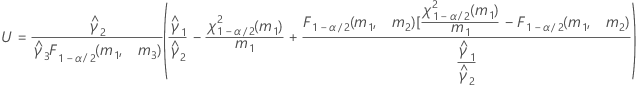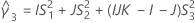Methoden und Formeln für die Varianzverhältnisse in Konfidenzintervallen in Gekreuzte Messsystemanalyse

Mit Prüfer

Wenn Prüfer- und Wechselwirkungsterm enthalten sind, gibt es zwei mögliche Berechnungsmethoden. Zunächst berechnet Minitab die Grenzen mit Hilfe der modifizierten Methode für große Stichproben (MLS). Wenn während der Berechnungen bestimmte Bedingungen nicht erfüllt sind, verwendet Minitab die Satterthwaite-Approximation. Zum Berechnen der einseitigen Konfidenzgrenzen muss α/2 in H und G durch α ersetzt werden.

MLS-Methode

Die zwei Bedingungen für das Vorhandensein von Untergrenze und Obergrenze bei Verwendung der MLS-Methode lauten wie folgt:

Wenn die beiden Bedingungen nicht erfüllt sind, kann Minitab die Untergrenze und die Obergrenze mit Hilfe dieser Methode nicht berechnen. Minitab berechnet die Untergrenze und die Obergrenze mit der Satterthwaite-Approximation.

Satterthwaite-Approximation

Es werden dieselben Formeln für die Untergrenze und die Obergrenze verwendet, U und O sind jedoch wie folgt definiert:

Ohne Prüferterm

Ohne Wechselwirkungsterm

Wenn Prüfer- und Wechselwirkungsterm enthalten sind, gibt es zwei mögliche Berechnungsmethoden. Zunächst berechnet Minitab die Grenzen mit Hilfe der modifizierten Methode für große Stichproben (MLS). Wenn während der Berechnungen bestimmte Bedingungen nicht erfüllt sind, verwendet Minitab die Satterthwaite-Approximation. Zum Berechnen der einseitigen Konfidenzgrenzen muss α/2 in H und G durch α ersetzt werden.

MLS-Methode

Die zwei Bedingungen für das Vorhandensein von Untergrenze und Obergrenze bei Verwendung der MLS-Methode lauten wie folgt:

Wenn die beiden Bedingungen nicht erfüllt sind, kann Minitab die Untergrenze und die Obergrenze mit Hilfe dieser Methode nicht berechnen. Minitab berechnet die Untergrenze und die Obergrenze mit der Satterthwaite-Approximation.

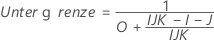
Satterthwaite-Approximation

Es werden dieselben Formeln für die Untergrenze und die Obergrenze verwendet, U und O sind jedoch wie folgt definiert:

Notation

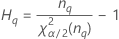
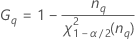
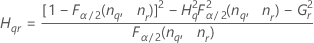
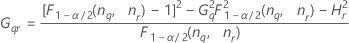
Begriff	Beschreibung
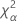	α *100-Perzentil der Chi-Quadrat-Verteilung mit nq Freiheitsgraden
J	Anzahl der Prüfer
I	Anzahl der Teile
K	Anzahl der Replikationen

Mit Wechselwirkungsterm

Es gibt zwei mögliche Berechnungsmethoden. Zunächst berechnet Minitab die Grenzen mit Hilfe der modifizierten Methode für große Stichproben (MLS). Wenn während der Berechnungen bestimmte Bedingungen nicht erfüllt sind, verwendet Minitab eine alternative Annäherung. Zum Berechnen der einseitigen Konfidenzgrenzen muss α/2 in H und G durch α ersetzt werden.

MLS-Methode

Die Untergrenze und die Obergrenze für ein approximiertes (1 – α) * 100%-Konfidenzintervall werden durch Lösen von quadratischen Gleichungen berechnet.

Wenn B²– 4AC < 0, weist die quadratische Gleichung keine Lösung auf. In diesem Fall schätzt Minitab die Konfidenzintervalle mit der zweiten Methode.

Zweite Methode

Die Untergrenze und die Obergrenze für ein approximiertes (1 – α) * 100%-Konfidenzintervall werden wie folgt berechnet:

Ohne Wechselwirkungsterm

Es gibt zwei mögliche Berechnungsmethoden. Zunächst berechnet Minitab die Grenzen mit Hilfe der modifizierten Methode für große Stichproben (MLS). Wenn während der Berechnungen bestimmte Bedingungen nicht erfüllt sind, verwendet Minitab eine alternative Annäherung. Zum Berechnen der einseitigen Konfidenzgrenzen muss α/2 in H und G durch α ersetzt werden.

MLS-Methode

Die Untergrenze und die Obergrenze für ein approximiertes (1 – α) * 100%-Konfidenzintervall werden durch Lösen von quadratischen Gleichungen berechnet. Die Untergrenze U entspricht J multipliziert mit der kleineren Lösung der folgenden Gleichung.

Die Obergrenze O entspricht J multipliziert mit der größeren Lösung der folgenden Gleichung.

Wenn B²– 4AC < 0, weist die quadratische Gleichung keine Lösung auf. In diesem Fall schätzt Minitab die Konfidenzintervalle mit der zweiten Methode.

Zweite Methode

Die Untergrenze und die Obergrenze für ein approximiertes (1 – α) * 100%-Konfidenzintervall werden wie folgt berechnet:

Notation

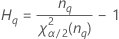
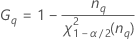
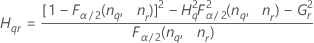
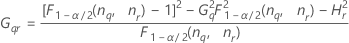
Begriff	Beschreibung
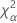	α *100-Perzentil der Chi-Quadrat-Verteilung mit nq Freiheitsgraden
J	Anzahl der Prüfer
I	Anzahl der Teile
K	Anzahl der Replikationen
a	I
b	J
c	(IJ – I –J)
d	IJ(K-1)
e	I – 1

Notation

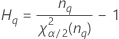
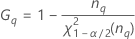
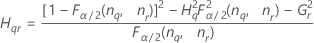
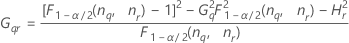
Begriff	Beschreibung
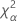	α *100-Perzentil der Chi-Quadrat-Verteilung mit nq Freiheitsgraden
J	Anzahl der Prüfer
I	Anzahl der Teile
K	Anzahl der Replikationen

Notation

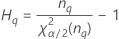
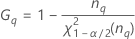
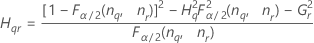
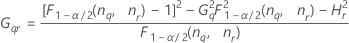
Begriff	Beschreibung
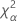	Das α *100-Perzentil der Chi-Quadrat-Verteilung mit nq-Freiheitsgraden
J	Anzahl der Prüfer
I	Anzahl der Teile
K	Anzahl der Replikationen

Mit Prüfer- und Wechselwirkungsterm

Es gibt zwei mögliche Berechnungsmethoden. Zunächst berechnet Minitab die Grenzen mit Hilfe der modifizierten Methode für große Stichproben (MLS). Wenn während der Berechnungen bestimmte Bedingungen nicht erfüllt sind, verwendet Minitab eine alternative Annäherung. Zum Berechnen der einseitigen Konfidenzgrenzen muss α/2 in H und G durch α ersetzt werden.

Ohne Prüferterm

Untergrenze = 1 – (Untergrenze für das Verhältnis zwischen der Varianz der Wiederholbarkeit und Gesamtvarianz)

Obergrenze = 1 – (Obergrenze für das Verhältnis zwischen der Varianz der Wiederholbarkeit und Gesamtvarianz)

Ohne Wechselwirkungsterm

Notation

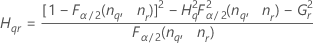
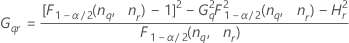
Begriff	Beschreibung
	α *100-Perzentil der Chi-Quadrat-Verteilung mit nq Freiheitsgraden
J	Anzahl der Prüfer
I	Anzahl der Teile
K	Anzahl der Replikationen