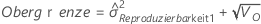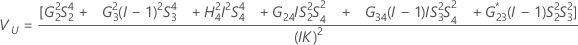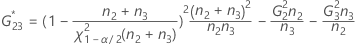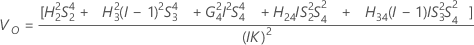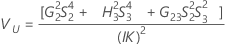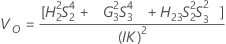In diesem Thema
- Übliche Notation und Regeln für Konfidenzintervalle in Messsystemanalysen
- Konfidenzintervall für die Varianzkomponente „Wiederholbarkeit“
- Konfidenzintervall für die Varianzkomponente „Reproduzierbarkeit“ (oder „Prüfer“)
- Konfidenzintervall für die Varianzkomponente „Prüfer“
- Konfidenzintervall für die Varianzkomponente der Wechselwirkung
- Konfidenzintervall für die Varianzkomponente „R&R (gesamt)“
- Konfidenzintervall für die Varianzkomponente „Zwischen den Teilen“
- Konfidenzintervall für die Varianzkomponente „Gesamt“
Übliche Notation und Regeln für Konfidenzintervalle in Messsystemanalysen
Für alle Varianzkomponenten dürfen die Unter- und Obergrenzen keine negativen Werte sein. Wenn die mit den Formeln berechneten Grenzen negativ sind, werden sie auf null gesetzt.
Für alle Verhältnisse zwischen 0 und 1 sollten auch die Unter- und Obergrenzen zwischen 0 und 1 liegen. Wenn die Grenzen außerhalb des zulässigen Bereichs liegen, werden sie entsprechend auf 0 oder 1 gesetzt.
Notation
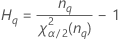
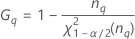
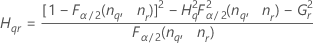
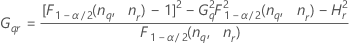
| Begriff | Beschreibung |
|---|---|
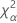 | α*100-Perzentil der Chi-Quadrat-Verteilung mit nq Freiheitsgraden |
| Fα(nq, nγ) | α*100-Perzentil der F-Verteilung mit nq und nγ Freiheitsgraden |
| I | Anzahl der Teile |
| J | Anzahl der Prüfer |
| K | Anzahl der Replikationen |
Für Freiheitsgrade:
Teile: n1=I–1
Prüfer: n2=J–1
Teile*Prüfer= n3=(I–1)(J–1)
Replikationen: n4=IJ(K–1)
MS Teile = S12
MS Prüfer = S22
MS Teil*Prüfer = S32
MS Replikationen = S42
Konfidenzintervall für die Varianzkomponente „Wiederholbarkeit“
Minitab berechnet die Untergrenze und die Obergrenze für ein exaktes (1 – α) * 100%-Konfidenzintervall. Zum Berechnen der einseitigen Konfidenzgrenzen muss α/2 in H und G durch α ersetzt werden.
Formeln
- Mit Prüfer
-
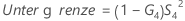
- Ohne Prüfer
-

- Ohne Wechselwirkungsterm
-

Notation
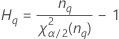
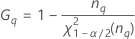
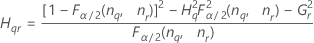
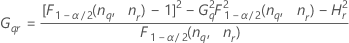
| Begriff | Beschreibung |
|---|---|
 | α *100-Perzentil der Chi-Quadrat-Verteilung mit nq Freiheitsgraden |
| J | Anzahl der Prüfer |
| I | Anzahl der Teile |
| K | Anzahl der Replikationen |
Konfidenzintervall für die Varianzkomponente „Reproduzierbarkeit“ (oder „Prüfer“)
Minitab berechnet die Untergrenze und die Obergrenze für ein approximiertes (1 – α) * 100%-Konfidenzintervall mit der modifizierten Methode für große Stichproben (MLS). Zum Berechnen der einseitigen Konfidenzgrenzen muss α/2 in H und G durch α ersetzt werden.
Formeln
- Mit Wechselwirkungsterm
-
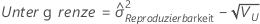
- Ohne Wechselwirkungsterm
-
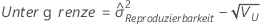
Notation
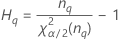
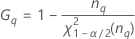
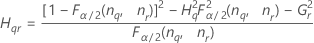
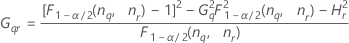
| Begriff | Beschreibung |
|---|---|
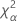 | α *100-Perzentil der Chi-Quadrat-Verteilung mit nq Freiheitsgraden |
| J | Anzahl der Prüfer |
| I | Anzahl der Teile |
| K | Anzahl der Replikationen |
Konfidenzintervall für die Varianzkomponente „Prüfer“
Minitab berechnet die Untergrenze und die Obergrenze für ein approximiertes (1 – α) * 100%-Konfidenzintervall mit Hilfe der modifizierten Methode für große Stichproben (MLS). Zum Berechnen der einseitigen Konfidenzgrenzen muss α/2 in H und G durch α ersetzt werden.
Formeln


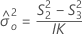
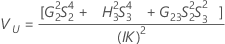
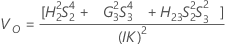
Notation
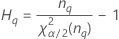
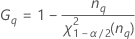
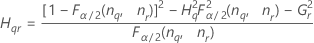
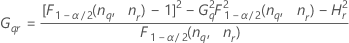
| Begriff | Beschreibung |
|---|---|
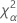 | α *100-Perzentil der Chi-Quadrat-Verteilung mit nq Freiheitsgraden |
| J | Anzahl der Prüfer |
| I | Anzahl der Teile |
| K | Anzahl der Replikationen |
Konfidenzintervall für die Varianzkomponente der Wechselwirkung
Minitab berechnet die Untergrenze und die Obergrenze für ein approximiertes (1 – α) * 100%-Konfidenzintervall mit Hilfe der modifizierten Methode für große Stichproben (MLS). Zum Berechnen der einseitigen Konfidenzgrenzen muss α/2 in H und G durch α ersetzt werden.
Formeln


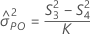
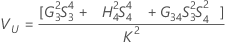
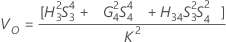
Notation


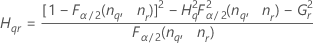

| Begriff | Beschreibung |
|---|---|
 | α *100-Perzentil der Chi-Quadrat-Verteilung mit nq Freiheitsgraden |
| J | Anzahl der Prüfer |
| I | Anzahl der Teile |
| K | Anzahl der Replikationen |
Konfidenzintervall für die Varianzkomponente „R&R (gesamt)“
Mit Prüfer- und Wechselwirkungsterm
Minitab berechnet die Untergrenze und die Obergrenze für ein approximiertes (1 – α) * 100%-Konfidenzintervall mit der modifizierten Methode für große Stichproben (MLS). Zum Berechnen der einseitigen Konfidenzgrenzen muss α/2 in H und G durch α ersetzt werden.





Ohne Prüferterm
Die Untergrenze und die Obergrenze für ein exaktes (1 – α) *100%-Konfidenzintervall werden wie folgt berechnet:


Ohne Wechselwirkungsterm
Minitab berechnet die Untergrenze und die Obergrenze für ein approximiertes (1 – α) * 100%-Konfidenzintervall mit der modifizierten Methode für große Stichproben (MLS). Zum Berechnen der einseitigen Konfidenzgrenzen muss α/2 in H und G durch α ersetzt werden.



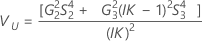
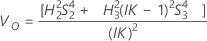
Notation
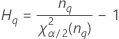
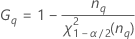
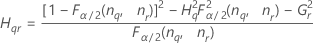
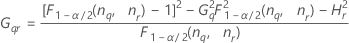
| Begriff | Beschreibung |
|---|---|
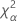 | α *100-Perzentil der Chi-Quadrat-Verteilung mit nq Freiheitsgraden |
| J | Anzahl der Prüfer |
| I | Anzahl der Teile |
| K | Anzahl der Replikationen |
Konfidenzintervall für die Varianzkomponente „Zwischen den Teilen“
Minitab berechnet die Untergrenze und die Obergrenze für ein approximiertes (1 – α) * 100%-Konfidenzintervall mit der modifizierten Methode für große Stichproben (MLS). Zum Berechnen der einseitigen Konfidenzgrenzen muss α/2 in H und G durch α ersetzt werden.
Mit Prüfer




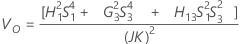
Ohne Prüfer


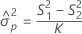


Ohne Wechselwirkung





Notation
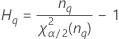


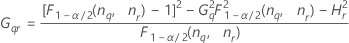
| Begriff | Beschreibung |
|---|---|
 | α *100-Perzentil der Chi-Quadrat-Verteilung mit nq Freiheitsgraden |
| J | Anzahl der Prüfer |
| I | Anzahl der Teile |
| K | Anzahl der Replikationen |
Konfidenzintervall für die Varianzkomponente „Gesamt“
Minitab berechnet die Untergrenze und die Obergrenze für ein approximiertes (1 – α) * 100%-Konfidenzintervall mit der modifizierten Methode für große Stichproben (MLS). Zum Berechnen der einseitigen Konfidenzgrenzen muss α/2 in H und G durch α ersetzt werden.
Mit Prüfer





Ohne Prüfer


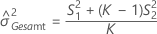


Ohne Wechselwirkungsterm



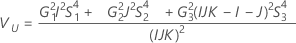
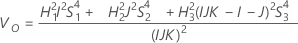
Notation
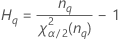

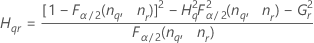
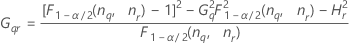
| Begriff | Beschreibung |
|---|---|
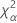 | α *100-Perzentil der Chi-Quadrat-Verteilung mit nq Freiheitsgraden |
| J | Anzahl der Prüfer |
| I | Anzahl der Teile |
| K | Anzahl der Replikationen |