In diesem Thema
VarKomp für die ANOVA-Methode
Die Streuungskomponente, die von jeder Quelle beigetragen wird.
Mit dem Interaktionsterm
Wenn die Wechselwirkung Prüfer*Teil im ANOVA-Modell enthalten ist, werden die Varianzkomponenten wie folgt berechnet:
- Wiederholbarkeit
-
Wiederholbarkeit = MSWiederholbarkeit
- Prüfer
-
- Prüfer*Teil
-
- Zwischen den Teilen
-
- Reproduzierbarkeit
- Reproduzierbarkeit = VarKompPrüfer +VarKompPrüfer*Teil
- R&R (gesamt)
- R&R (gesamt) = VarKompWiederholbarkeit + VarKompReproduzierbarkeit
- Gesamtstreuung
- Gesamtstreuung = VarKompR&R (gesamt) + VarKompZwischen den Teilen
Ohne den Interaktionsterm
Wenn die Wechselwirkung Prüfer*Teil nicht im ANOVA-Modell enthalten ist, werden die Varianzkomponenten wie folgt berechnet:
- Wiederholbarkeit
-
Wiederholbarkeit = MSWiederholbarkeit
- Prüfer
-
- Zwischen den Teilen
-
- Reproduzierbarkeit
- Reproduzierbarkeit = VarKompPrüfer
- R&R (gesamt)
- R&R (gesamt) = VarKompWiederholbarkeit + VarKompReproduzierbarkeit
- Gesamtstreuung
- Gesamtstreuung = VarKompR&R (gesamt) + VarKompZwischen den Teilen
Wenn eine Varianzkomponente negativ ist, wird sie von der Messsystemanalyse als null angegeben.
Varianz für die X-quer/R-Methode
Die Varianz, die von jeder Quelle beigetragen wird.
- Wiederholbarkeit
- Streuung aufgrund der Messgeräte; die Standardabweichung wird wie folgt berechnet:
-
- Reproduzierbarkeit
-
Streuung aufgrund der Prüfer; die Standardabweichung wird wie folgt berechnet:
-
Begriff Beschreibung 
durchschnittlicher Messwert für Prüfer i a Anzahl der Teile r Anzahl der Versuche d2 d2 = d2* aus Appendix C1. Verwenden Sie beim Bestimmen dieses Werts g = 1 und m = (Anzahl der Prüfer). - Zwischen den Teilen
-
Die Standardabweichung wird wie folgt berechnet:
- R&R (gesamt)
-
Die Standardabweichung wird wie folgt berechnet:
- Gesamtstreuung
-
Die Standardabweichung wird wie folgt berechnet:
%Beitrag
„%Beitrag“ ist der Prozentsatz der einzelnen Varianzkomponenten an der Gesamtstreuung. Dieser Wert wird berechnet, indem die Varianzkomponente der betreffenden Quelle durch die Gesamtstreuung dividiert und anschließend mit 100 multipliziert wird, um ihn als Prozentsatz auszudrücken. „%Beitrag“ wird berechnet, indem jede Varianzkomponente durch die Gesamtstreuung dividiert und mit 100 multipliziert wird. Die Summe der Prozentsätze in dieser Spalte beträgt 100.
StdAbw
„StdAbw“ ist die Standardabweichung für die einzelnen Streuungsquellen. Die Standardabweichung ist die Quadratwurzel der Varianzkomponente für die betreffende Quelle.
- Wenn
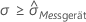, dann ist die Gesamtstandardabweichung gleich σ und 
. - Andernfalls verwendet Minitab die Daten zum Schätzen der Gesamtstandardabweichung und
.
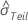| Begriff | Beschreibung |
|---|---|
 | historische Standardabweichung |
 | aus den Daten berechnete Gesamtstandardabweichung des Messsystems |
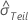 | Standardabweichung zwischen den Teilen |
Streuung in Untersuchung
Die Streuung in der Untersuchung wird berechnet, indem die Standardabweichung für jede Streuungsquelle mit 6 oder einem anderen Multiplikator multipliziert wird, den Sie in Streuung in Untersuchung angeben.
Im Allgemeinen wird die Prozessstreuung als 6s definiert, wobei s die Standardabweichung als Schätzwert der Standardabweichung der Grundgesamtheit (bezeichnet als σ oder Sigma) ist. Wenn die Daten normalverteilt sind, liegen etwa 99,73 % der Daten innerhalb von 6 Standardabweichungen des Mittelwerts. Wenn Sie einen anderen Prozentsatz der Daten festlegen möchten, geben Sie einen anderen Multiplikator für die Standardabweichung an. Wenn Sie beispielsweise die Lage von 99 % der Daten ermitteln möchten, geben Sie anstelle des Standardmultiplikators 6 den Multiplikator 5,15 an.
%Streuung in Untersuchung und KI
„%Streuung in Unters.“ wird berechnet, indem die Streuung in der Untersuchung für jede Streuungsquelle durch die Gesamtstreuung dividiert und das Ergebnis mit 100 multipliziert wird.
„%Streuung in Unters.“ ist die Quadratwurzel der berechneten Varianzkomponente (VarKomp) für die betreffende Quelle. Daher summieren sich die Werte für „%Beitrag“ für „VarKomp“ auf 100, während dies bei den Werten für „%Streuung in Unters.“ nicht der Fall ist.
Konfidenzintervall
Wenn U und O die Unter- und Obergrenze von % Beitrag darstellen, ist das Konfidenzintervall für das entsprechende % Streuung in Untersuchung:
%Toleranz und KI
%Toleranz gibt die prozentuale Toleranz für die einzelnen Komponenten an.
Wenn die Toleranz (obere Spezifikationsgrenze – untere Spezifikationsgrenze) angegeben ist, wird %Toleranz berechnet, indem die Streuung in Untersuchung für jede Komponente durch die angegebene Toleranz dividiert wird.
Wenn nur eine Spezifikationsgrenze angegeben ist, entspricht die prozentuale Toleranz der halben Streuung in der Untersuchung für jede Komponente dividiert durch die einseitige Toleranz. Die einseitige Toleranz ist der absolute Wert der angegebenen Spezifikationsgrenze subtrahiert vom Durchschnitt aller Messwerte.
Minitab zeigt diesen Wert nur an, wenn Sie im Unterdialogfeld „Optionen“ die Prozesstoleranz (obere Spezifikationsgrenze – untere Spezifikationsgrenze) oder eine Spezifikationsgrenze angeben.
Konfidenzintervall
Wenn U und O die Untergrenze und die Obergrenze einer Varianzkomponente darstellen, ist das Konfidenzintervall für die entsprechende prozentuale Toleranz:
| Begriff | Beschreibung |
|---|---|
| k | k ist die Untersuchungskonstante; der Standardwert beträgt 6. |
%Prozess und KI
%Prozess ist der Prozentsatz der Prozessstreuung; dieser wird als Verhältnis zwischen der geschätzten Standardabweichung und der historischen Standardabweichung berechnet.
Minitab zeigt diesen Wert nur an, wenn Sie im Unterdialogfeld „Optionen“ eine historische Standardabweichung eingeben.
Konfidenzintervall
Wenn U und O die Untergrenze und die Obergrenze einer Varianzkomponente darstellen, ist das Konfidenzintervall für die entsprechende Prozessstreuung:
| Begriff | Beschreibung |
|---|---|
| k | k ist die Untersuchungskonstante; der Standardwert beträgt 6. |
