Interpretieren der wichtigsten Ergebnisse für Gekreuzte Messsystemanalyse

Führen Sie die folgenden Schritte aus, um eine gekreuzte Messsystemanalyse zu interpretieren. Zu den wichtigsten Ausgaben zählen Schätzwerte der Streuung sowie Grafiken der Messwerte und der Messwertstreuung.

In diesem Thema

Schritt 1: Signifikante Faktoren und Wechselwirkungen anhand der ANOVA-Tabelle bestimmen
Schritt 2: Bewerten der Streuung für jede Messfehlerquelle
Schritt 3: Grafiken auf weitere Informationen zur Messsystemanalyse untersuchen

Schritt 1: Signifikante Faktoren und Wechselwirkungen anhand der ANOVA-Tabelle bestimmen

Bestimmen Sie anhand der ANOVA-Tabelle, welche Streuungsquellen signifikant sind. Die ANOVA-Tabelle enthält in der Spalte „Quelle“ die folgenden Terme:

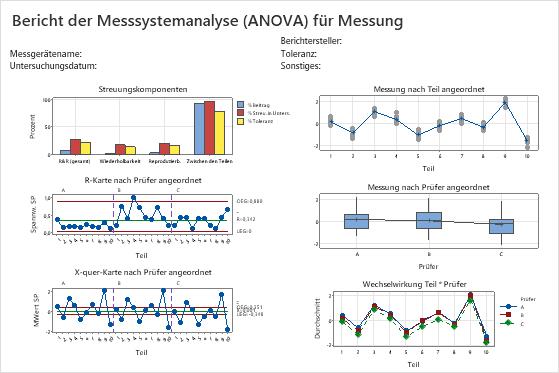
Teil: Die Streuung, die auf die Teile zurückzuführen ist.
Prüfer: Die Streuung, die auf die Prüfer zurückzuführen ist.
Prüfer*Teil: Die Streuung, die auf die Wechselwirkung zwischen Prüfer und Teil zurückzuführen ist. Eine Wechselwirkung besteht, wenn ein Prüfer verschiedene Teile unterschiedlich misst.
Fehler oder Wiederholbarkeit: Die Streuung, die nicht durch die Teile, die Prüfer oder die Wechselwirkung zwischen Prüfer und Teil erklärt wird.

Hinweis

Wenn Sie im Feld Analysemethode die Option „X-quer/R“ auswählen, zeigt Minitab die ANOVA-Tabelle nicht an.

Wenn der p-Wert für die Wechselwirkung zwischen Prüfer und Teil 0,05 oder größer ist, entfernt Minitab die Wechselwirkung, da sie nicht signifikant ist, und erstellt eine zweite ANOVA-Tabelle ohne die Wechselwirkung.

Zweifache ANOVA-Tabelle mit Wechselwirkungen Quelle DF SS MS F p Teil 9 88,3619 9,81799 492,291 0,000 Prüfer 2 3,1673 1,58363 79,406 0,000 Teil * Prüfer 18 0,3590 0,01994 0,434 0,974 Wiederholbarkeit 60 2,7589 0,04598 Gesamt 89 94,6471 α für Ausschluss des Wechselwirkungsterms = 0,05

Zweifache ANOVA-Tabelle ohne Wechselwirkungen Quelle DF SS MS F p Teil 9 88,3619 9,81799 245,614 0,000 Prüfer 2 3,1673 1,58363 39,617 0,000 Wiederholbarkeit 78 3,1179 0,03997 Gesamt 89 94,6471

Varianzkomponenten %Beitrag (der Quelle VarKomp VarKomp) R&R (gesamt) 0,09143 7,76 Wiederholbarkeit 0,03997 3,39 Reproduzierbarkeit 0,05146 4,37 Prüfer 0,05146 4,37 Zwischen den Teilen 1,08645 92,24 Gesamtstreuung 1,17788 100,00

Wichtigstes Ergebnis: p-Wert

In diesen Ergebnissen ist der p-Wert gleich 0,974. Daher erstellt Minitab eine zweite zweifache ANOVA-Tabelle, in der diese Wechselwirkung nicht im endgültigen Modell enthalten ist.

Schritt 2: Bewerten der Streuung für jede Messfehlerquelle

Mit den Varianzkomponenten (VarKomp) und „%Beitrag“ können Sie die Streuung für jede Messfehlerquelle bewerten. Die folgenden Quellen sind vorhanden:

R&R (gesamt): Die Summe der Varianzkomponenten für Wiederholbarkeit und Reproduzierbarkeit.
Wiederholbarkeit: Die Streuung in den Messwerten, wenn dasselbe Teil mehrmals vom selben Prüfer gemessen wird.
Reproduzierbarkeit: Die Streuung in den Messwerten, wenn verschiedene Prüfer dasselbe Teil messen.
Zwischen den Teilen: Die Streuung in den Messwerten, die auf verschiedene Teile zurückzuführen ist.

Im Idealfall sollte nur ein sehr geringer Teil der Streuung auf die Wiederholbarkeit und die Reproduzierbarkeit zurückzuführen sein. Die Differenzen zwischen den Teilen sollten einen Großteil der Streuung erklären.

Varianzkomponenten %Beitrag (der Quelle VarKomp VarKomp) R&R (gesamt) 0,0020816 6,82 Wiederholbarkeit 0,0011541 3,78 Reproduzierbarkeit 0,0009275 3,04 Zwischen den Teilen 0,0284585 93,18 Gesamtstreuung 0,0305401 100,00

Wichtigste Ergebnisse: VarKomp, %Beitrag

Der %Beitrag für die Streuung zwischen den Teilen beträgt 93,18 %. Minitab dividiert die Streuung zwischen den Teilen (ca. 0,0285) durch die Gesamtstreuung (ca. 0,0305) und multipliziert das Ergebnis mit 100 %. Wenn „%Beitrag“ für die Streuung zwischen den Teilen hoch ist, kann das Messgerät zuverlässig zwischen Teilen unterscheiden.

R&R (gesamt) Streu. in Unters. %Streu. in Unters. Quelle StdAbw (6 × SA) (%SU) R&R (gesamt) 0,045625 0,27375 26,11 Wiederholbarkeit 0,033972 0,20383 19,44 Reproduzierbarkeit 0,030455 0,18273 17,43 Zwischen den Teilen 0,168696 1,01218 96,53 Gesamtstreuung 0,174757 1,04854 100,00 %Toleranz Quelle (SU/Tol) R&R (gesamt) 27,37 Wiederholbarkeit 20,38 Reproduzierbarkeit 18,27 Zwischen den Teilen 101,22 Gesamtstreuung 104,85 Die historische Standardabweichung wird verwendet, um einige der Werte für StdAbw, Streuung in Untersuchung und %Streuung in Untersuchung zu berechnen. Die Werte für %Prozess werden nicht angezeigt, da sie den Werten für %Streuung in Untersuchung entsprechen.

Wichtigstes Ergebnis: %Streuung in Untersuchung

Verwenden Sie den Prozentsatz der Streuung in der Untersuchung („%Streuung in Unters.“), um die Streuung des Messsystems mit der Gesamtstreuung zu vergleichen. Für den Wert von „%Streuung in Unters.“ wird die Prozessstreuung verwendet, die als das Sechsfache der Standardabweichung im Prozess definiert ist. Minitab zeigt die Spalte „%Toleranz“ an, wenn Sie einen Toleranzwert eingeben, und die Spalte „%Prozess“, wenn Sie eine historische Standardabweichung eingeben.

Gemäß den Richtlinien der AIAG ist das Messsystem akzeptabel, wenn die Streuung im Messsystem weniger als 10 % der Prozessstreuung beträgt. Da die Werte für %Streuung in Untersuchung, %Toleranz und %Prozess alle größer als 10 % sind, muss das Messsystem möglicherweise verbessert werden. Weitere Informationen finden Sie unter Ist das Messsystem akzeptabel?.

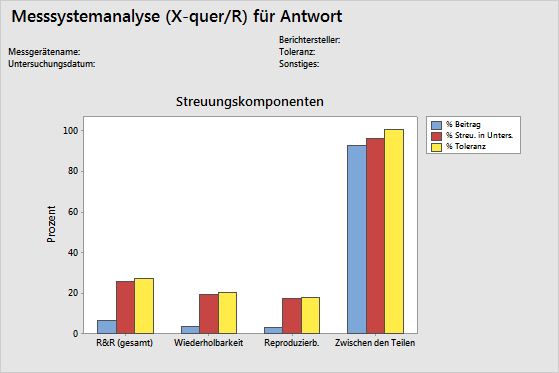
Wichtigstes Ergebnis: Grafik „Streuungskomponenten“

Die Grafik „Streuungskomponenten“ veranschaulicht die Streuung aus den einzelnen Quellen von Messfehlern. Minitab zeigt Balken für „%Toleranz“ an, wenn Sie einen Toleranzwert eingeben, und Balken für „%Prozess“, wenn Sie eine historische Standardabweichung eingeben.

Dieses Diagramm veranschaulicht, dass die Streuung zwischen den Teilen größer als die Streuung aus Wiederholbarkeit und Reproduzierbarkeit ist. Die Gesamtstreuung beträgt jedoch mehr als 10 % und ist möglicherweise inakzeptabel.

Schritt 3: Grafiken auf weitere Informationen zur Messsystemanalyse untersuchen

Die Grafiken der Messsystemanalyse liefern Informationen zum Messsystem.

Grafik „Streuungskomponenten“: Diese Grafik zeigt, ob die größte Streuungskomponente die Streuung zwischen den Teilen ist.; In einem akzeptablen Messsystem ist die größte Streuungskomponente die Streuung zwischen den Teilen.
R-Karte nach Prüfer angeordnet: Diese Regelkarte veranschaulicht, ob Punkte über der oberen Eingriffsgrenze liegen.; Wenn die Prüfer beständig messen, liegen die Punkte innerhalb der Eingriffsgrenzen.
X-quer-Karte nach Prüfer angeordnet: Diese Regelkarte veranschaulicht, ob die meisten Punkte außerhalb der Eingriffsgrenzen liegen.; Die für eine Messsystemanalyse ausgewählten Teile sollten die typische Streuung zwischen den Teilen darstellen. Daher sollten Sie eine größere Streuung zwischen den Durchschnittswerten der Teile erwarten, und die Grafik sollte zeigen, dass die meisten Punkte außerhalb der Eingriffsgrenzen liegen.
Grafik „Messwerte nach Teilen“: In dieser Grafik wird veranschaulicht, ob mehrere Messwerte für jedes Teil nah beieinander liegen.; Mehrere nah beieinander liegende Messwerte für jedes Teil weisen auf eine geringe Streuung zwischen den Messwerten des jeweiligen Teils hin.
Grafik „Messwerte nach Prüfer“: Dieses Grafik veranschaulicht, ob die Unterschiede zwischen den Prüfern im Vergleich zu den Unterschieden zwischen den Teilen klein sind.; Eine horizontale Gerade über verschiedene Prüfer hinweg zeigt, dass die mittleren Messwerte für jeden Prüfer gleich sind. Im Idealfall variieren die Messwerte für jeden Prüfer um den gleichen Beitrag.
Grafik der Wechselwirkung Prüfer*Teil: Diese Grafik veranschaulicht, ob die Linien, die die Messwerte der einzelnen Prüfer verbinden, übereinstimmen oder einander schneiden.; Zusammenfallende Linien zeigen an, dass die Prüfer gleich messen. Linien, die nicht parallel verlaufen oder einander schneiden, verweisen darauf, dass die Fähigkeit eines Prüfers, ein Teil beständig zu messen, vom jeweils gemessenen Teil abhängt. Eine Linie, die durchgehend höher oder niedriger als die übrigen liegt, zeigt an, dass ein Prüfer eine systematische Messabweichung beiträgt, indem er beständig zu hohe oder zu niedrige Messwerte erfasst.