In diesem Thema
Systematische Messabweichung
Die systematische Messabweichung wird als Differenz zwischen dem bekannten Standardwert eines Referenzteils und dem beobachteten Durchschnittsmesswert berechnet.
- Punktschätzung der systematischen Messabweichung mit einer unteren Toleranzgrenze
- Systematische Messabweichung = Untergrenze + Schnittpunkt mit y-Achse / Steigung
- Punktschätzung der systematischen Messabweichung mit einer oberen Toleranzgrenze
- Systematische Messabweichung = Obergrenze + Schnittpunkt mit y-Achse / Steigung
Der Schnittpunkt mit der y-Achse und die Steigung in beiden Formeln stammen von der Anpassungslinie im Wahrscheinlichkeitsnetz.
Minitab führt eine Regression des Z-Werts Φ-1(Wahrscheinlichkeit (Annahme)) auf Referenzwerte xT aus, um den Schnittpunkt mit der y-Achse und die Steigung zu berechnen.
Wiederholbarkeit vor Korrektur
Die Wiederholbarkeit vor Korrektur ist die Wiederholbarkeit, die vor der Korrektur von Überschätzungen berechnet wird.
Formel
Minitab schätzt die Wiederholbarkeit vor Korrektur wie folgt:

Notation
| Begriff | Beschreibung |
|---|---|
| XT | stellt die geschätzten Referenzwerte bei den Annahmewahrscheinlichkeiten 0,995 und 0,005 dar, die aus der Anpassungslinie des Wahrscheinlichkeitsnetzes berechnet werden. |
Wiederholbarkeit
Als Wiederholbarkeit wird der Streuungsgrad im Messsystem bezeichnet, der auf das Messgerät zurückzuführen ist. Bei einer Messsystemanalyse für attributive Daten wird eine Regression der Annahmewahrscheinlichkeit auf die Referenzwerte ausgeführt, um die Wiederholbarkeit zu ermitteln.
Die Wiederholbarkeit vor Korrektur ist die Wiederholbarkeit, die vor der Korrektur von Überschätzungen berechnet wird. Minitab dividiert die Schätzwerte der Wiederholbarkeit durch den Korrekturfaktur 1,08, um die korrigierte Wiederholbarkeit zu berechnen.
Formel
Minitab schätzt die Wiederholbarkeit wie folgt:
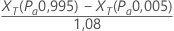
Notation
| Begriff | Beschreibung |
|---|---|
| XT | stellt die geschätzten Referenzwerte bei den Annahmewahrscheinlichkeiten 0,995 und 0,005 dar, die aus der Anpassungslinie des Wahrscheinlichkeitsnetzes berechnet werden. |
Der Nenner 1,08 ist der empfohlene Korrekturfaktor der Automotive Industry Action Group1 Minitab verwendet den korrigierten Wiederholbarkeitswert beim Test, ob die systematische Messabweichung gleich 0 ist.
T für die AIAG-Methode
Formel
Zum Testen auf systematische Messabweichung = 0 mit der Regressionsmethode verwendet Minitab die folgende Formel:
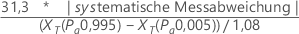
Notation
| Begriff | Beschreibung |
|---|---|
| XT | stellt die geschätzten Referenzwerte bei den Annahmewahrscheinlichkeiten 0,995 und 0,005 dar, die aus der Anpassungslinie im Wahrscheinlichkeitsnetz berechnet werden. |
- 6 Teile weisen mehr als 0 und weniger als 20 Annahmen auf.
- 1 Teil weist 0 Annahmen auf.
- 1 Teil weist 20 Annahmen auf.
T für Regressionsmethode
Formel
Zum Testen auf systematische Messabweichung = 0 mit der Regressionsmethode verwendet Minitab die folgende Formel:
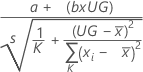
Notation
| Begriff | Beschreibung |
|---|---|
| a | Schnittpunkt der Anpassungslinie mit der y-Achse im Wahrscheinlichkeitsnetz |
| b | Steigung der Anpassungslinie im Wahrscheinlichkeitsnetz |
| UG | untere Toleranzgrenze |
| s | Standardabweichung der Fehler, die anhand der Anpassungslinie berechnet wird |
| K | Anzahl der Teile |
| xi | Referenzwert jedes Teils |
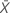 | Mittelwert der Referenzwerte |
DF für AIAG-Methode
Der Wert für die Freiheitsgrade wird verwendet, um den p-Wert zu ermitteln.
DF = N – 1.
Notation
| Begriff | Beschreibung |
|---|---|
| N | Anzahl der Versuche |
DF für Regressionsmethode
Der Wert für die Freiheitsgrade wird verwendet, um den p-Wert zu ermitteln.
DF = N – 2.
Notation
| Begriff | Beschreibung |
|---|---|
| N | Anzahl der Punkte zum Berechnen der Anpassungslinie |
p-Wert
p-Werte werden in Hypothesentests verwendet, um Ihnen die Entscheidung zu ermöglichen, ob eine Nullhypothese zurückgewiesen oder nicht zurückgewiesen werden sollte.
Um zu bestimmen, ob die systematische Messabweichung des Messsystems statistisch signifikant ist, vergleichen Sie den p-Wert mit dem Signifikanzniveau. In der Regel ist ein Signifikanzniveau (als α oder Alpha bezeichnet) von 0,05 gut geeignet. Ein Signifikanzniveau von 0,05 bedeutet ein Risiko der Schlussfolgerung, dass eine signifikante systematische Messabweichung vorliegt, wenn dies tatsächlich nicht der Fall ist, von 5 %.
Anpassungslinie
Die Anpassungslinie ist eine Regressionslinie, mit der die Beziehung zwischen den Annahmewahrscheinlichkeiten und den Referenzwerten der gemessenen Teile untersucht wird.
Die allgemeine Formel einer Anpassungslinie lautet: Y = b0 + b1 X
Minitab führt eine Regression des Z-Werts Φ-1(Wahrscheinlichkeit (Annahme)) auf die Referenzwerte XT aus, um den Schnittpunkt mit der y-Achse und die Steigung zu ermitteln.
Notation
| Begriff | Beschreibung |
|---|---|
| b0 | Schnittpunkt mit der y-Achse: Konstante, welche die vertikale Lage der Regressionslinie bestimmt |
| b1 | Steigung der Regressionslinie |
| X | Prädiktorwert |
R-Qd für Anpassungslinie
R-Qd für Anpassungslinie ist der Determinationskoeffizient, mit dem überprüft wird, ob die Anpassungslinie die Daten zutreffend wiedergibt. Der R-Qd-Wert (R2) für die angepasste Regressionslinie gibt die prozentuale Streuung in den Werten der Antwortvariablen für die Annahmewahrscheinlichkeit an, die durch das Regressionsmodell erklärt wird.
R2 = 1 - (SS Fehler / SS gesamt)
Notation
| Begriff | Beschreibung |
|---|---|
| SS Fehler | Summe der Quadrate für den Fehler |
| SS gesamt | Gesamtsumme der Quadrate |
