In diesem Thema
Schritt 1: Systematische Messabweichung im Messsystem bewerten
Die systematische Messabweichung ist ein Maß für die Genauigkeit eines Messsystems. Die systematische Messabweichung wird als Differenz zwischen dem bekannten Standardwert eines Referenzteils und dem beobachteten Durchschnittsmesswert berechnet. Ein niedriger Wert der systematischen Messabweichung bedeutet, dass das Messsystem für attributive Daten Teile nahezu übereinstimmend mit den Referenzwerten misst.
Um zu bestimmen, ob die systematische Messabweichung des Messsystems statistisch signifikant ist, vergleichen Sie den p-Wert mit dem Signifikanzniveau. In der Regel ist ein Signifikanzniveau (als α oder Alpha bezeichnet) von 0,05 gut geeignet. Ein Signifikanzniveau von 0,05 bedeutet ein Risiko der Schlussfolgerung, dass eine signifikante systematische Messabweichung vorliegt, wenn dies tatsächlich nicht der Fall ist, von 5 %.
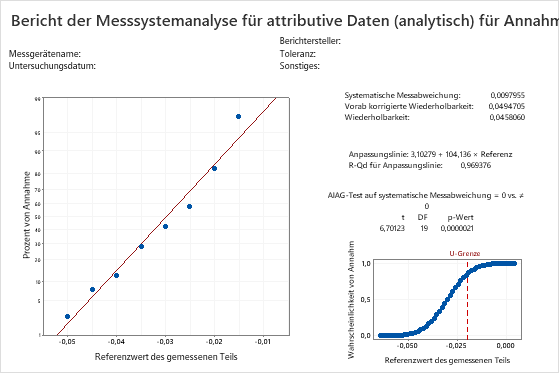
Wichtigstes Ergebnis: p-Wert
Für dieses Beispiel ist die systematische Messabweichung gleich 0,0097955, und der p-Wert beträgt 0,0000021. Da der p-Wert kleiner als das Signifikanzniveau 0,05 ist, weisen Sie die Nullhypothese zurück, dass die systematische Messabweichung 0 ist. Sie schließen, dass die systematische Messabweichung in diesem Messsystem statistisch signifikant ist.
Hinweis
Wenn Sie die Standardeinstellung so ändern, dass anstelle der AIAG-Methode die Regressionsmethode verwendet wird, kann der p-Wert leicht abweichen.
Schritt 2: Darstellung der Anpassungslinie auswerten
Im Wahrscheinlichkeitsnetz für Normalverteilung wird der Prozentsatz der Annahmen für jeden Referenzwert dargestellt. Da keine tatsächlichen Messwerte vom Messsystem verfügbar sind, um die systematische Messabweichung und Wiederholbarkeit zu schätzen, berechnet Minitab die systematische Messabweichung und Wiederholbarkeit durch Anpassen der Normalverteilungskurve mit Hilfe der berechneten Annahmewahrscheinlichkeiten und dem bekannten Referenzwert für alle Teile.
Wenn die Messfehler einer Normalverteilung folgen, liegen die berechneten Wahrscheinlichkeiten entlang einer Geraden. Eine Regressionslinie wird an die Wahrscheinlichkeiten angepasst.
Der R-Qd-Wert (R2) für die angepasste Regressionslinie gibt die prozentuale Streuung in den Werten der Antwortvariablen für die Annahmewahrscheinlichkeit an, die durch das Regressionsmodell erklärt wird. R2 kann im Bereich von 0 bis 100 % liegen. Im Allgemeinen gilt: Je höher der R2-Wert, desto besser ist das Modell an die Daten angepasst. R2-Werte, die größer als 90 % sind, verweisen in der Regel auf eine sehr gute Anpassung an die Daten.

Wichtigstes Ergebnis: R-Qd
Für dieses Beispiel beträgt der R-Qd-Wert 0,969376. Die Anpassungslinie ist sehr gut an die Daten angepasst, und das Modell erklärt nahezu 97 % der Varianz.
Schritt 3: Leistungskurve des Messsystems auswerten
Die Leistungskurve des Messgeräts stellt die geschätzte Annahmewahrscheinlichkeit als Funktion des Referenzwerts für das Prüfobjekt dar. Die vertikale Referenzlinie zeigt die für die Analyse eingegebenen Grenzwerte an.
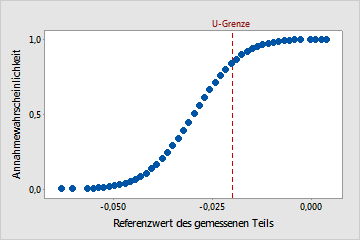
Für diese Daten besteht eine relativ hohe Wahrscheinlichkeit (annähernd 0,84), dass ein Prüfobjekt an der unteren Toleranzgrenze von –0,020 angenommen wird. Die Annahmerate ist jedoch bei Werten knapp unterhalb der Toleranzgrenze ebenfalls relativ hoch. Wenn die untere Toleranzgrenze kritisch ist, muss das Messsystem verbessert werden.
