In diesem Thema
Kendall-Koeffizient der Konkordanz
Verwenden Sie die Kendall-Statistik mit ordinalen Daten, die mindestens drei Stufen aufweisen.
In der Beschreibung der Methode wird angenommen, dass jeder Prüfer jedes Prüfobjekt einmal einstuft und dass k Prüfer pro Prüfobjekt vorhanden sind; diese Annahmen schränken die Allgemeingültigkeit nicht ein. Zum Berechnen des Kendall-Koeffizienten stellen die k Prüfer dann die k Versuche für jeden Prüfer dar.
Angenommen, die Daten sind in einer k x N-Tabelle angeordnet, in der jede Zeile die Ränge darstellt, die den N Prüfobjekten von einem bestimmten Prüfer zugewiesen werden.
Formeln
Wenn der tatsächliche Standard nicht bekannt ist, schätzt Minitab den Kendall-Koeffizienten wie folgt:
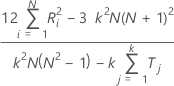
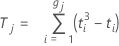
Notation
| Begriff | Beschreibung |
|---|---|
| N | Anzahl der Prüfobjekte |
| Σ Ri2 | Summe der Quadratsummen der Ränge für jedes der in Rangfolge vorliegenden N Prüfobjekte |
| K | Anzahl der Prüfer |
| Tj | Tj weist gebundenen Beobachtungen den Durchschnitt der Bewertungen zu. |
| Begriff | Beschreibung |
|---|---|
| ti | Anzahl der gebundenen Ränge in der i-ten Gruppierung von Bindungen |
| gj | Anzahl der Gruppen von Bindungen im j-ten Satz von Rängen |
Testen der Signifikanz des Kendall-Koeffizienten der Konkordanz
Um die Signifikanz des Kendall-Koeffizienten zu testen, verwenden Sie Folgendes:
c 2= k (N – 1) W
Notation
| Begriff | Beschreibung |
|---|---|
| c 2 | weist eine Chi-Quadrat-Verteilung mit N – 1 Freiheitsgraden auf |
| k | Anzahl der Prüfer |
| N | Anzahl der Prüfobjekte |
| W | berechneter Kendall-Koeffizient |
Kendall-Korrelationskoeffizient
Verwenden Sie die Kendall-Statistik mit ordinalen Daten, die mindestens drei Stufen aufweisen.
In der Beschreibung der Methode wird angenommen, dass jeder Prüfer jedes Prüfobjekt einmal einstuft und dass k Prüfer pro Prüfobjekt vorhanden sind; diese Annahmen schränken die Allgemeingültigkeit nicht ein. Zum Berechnen des Kendall-Korrelationskoeffizienten stellen die k Prüfer dann die k Versuche für alle Prüfer dar.
Wenn der tatsächliche Standard bekannt ist, schätzt Minitab den Kendall-Korrelationskoeffizienten, indem der Durchschnitt der Kendall-Koeffizienten zwischen jedem Prüfer und dem Standard berechnet wird.
Der Kendall-Korrelationskoeffizient für die Übereinstimmung der Versuche mit dem bekannten Standard ist der versuchsübergreifende Durchschnitt der Kendall-Korrelationskoeffizienten.
Formeln
Minitab berechnet den Kendall-Koeffizienten zwischen jedem Versuch und dem Standard wie folgt:

Notation
| Begriff | Beschreibung |
|---|---|
| TX | Anzahl der gebundenen Paare bei X = 0,5 Σi ni+ (ni+– 1) |
| TY | Anzahl der gebundenen Paare bei Y = 0,5 Σj n+j (n+j– 1) |
| C | Anzahl der konkordanten Paare = Σi<kΣj<l nij nkl |
| D | Anzahl der diskordanten Paare = Σi<kΣj>l nij nkl |
| Begriff | Beschreibung |
|---|---|
| ni+ | Anzahl der Beobachtungen in der i-ten Zeile |
| n+j | Anzahl der Beobachtungen in der j-ten Spalte |
| nij | Beobachtungen in der Zelle, die der i-ten Zeile und der j-Spalte entspricht |
| nkl | Beobachtungen in der Zelle, die der k-ten Zeile und der l-ten Spalte entspricht |
| n++ | Gesamtzahl der Beobachtungen |
Literaturhinweis
A. Agresti (1984). Analysis of Ordinal Categorical Data, John Wiley & Sons.
Testen der Signifikanz des Kendall-Korrelationskoeffizienten
Formel
Um die Signifikanz des Kendall-Koeffizienten zu testen, wenn der tatsächliche Standard bekannt ist, verwenden Sie Folgendes:
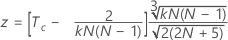
verwenden Sie Folgendes:
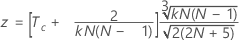
Notation
| Begriff | Beschreibung |
|---|---|
| Tc | Durchschnitt der Kendall-Korrelationskoeffizienten zwischen jedem Prüfer und dem Standard |
| N | Gesamtzahl der Prüfobjekte |
| k | Anzahl der Prüfer |
