Methoden und Formeln für Kappa-Statistiken für Prüferübereinstimmung bei attributiven Daten

Wählen Sie die gewünschte Methode oder Formel aus.

In diesem Thema

Cohen-Kappa-Statistik (unbekannter Standard)
Cohen-Kappa-Statistik (bekannter Standard)
Testen der Signifikanz des Cohen-Kappa
Fleiss-Kappa-Statistik (unbekannter Standard)
Testen der Signifikanz des Fleiss-Kappa (unbekannter Standard)
Fleiss-Kappa-Statistik (bekannter Standard)
Testen der Signifikanz des Fleiss-Kappa (bekannter Standard)

Cohen-Kappa-Statistik (unbekannter Standard)

Wenn die Klassifikationen nominal sind, verwenden Sie die Cohen-Kappa-Statistik. Wenn der Standard nicht bekannt ist und Sie festlegen, dass Minitab die Cohen-Kappa-Statistik berechnet, erfolgt dies, sofern die Daten die folgenden Bedingungen erfüllen:

Innerhalb der Prüfer: Es gibt genau zwei Versuche pro Prüfer.
Zwischen Prüfern: Es gibt genau zwei Prüfer, die jeweils nur über einen Versuch verfügen.

Für einen bestimmten Wert der Antwortvariablen kann Kappa berechnet werden, indem alle Werte der Antwortvariablen, die nicht diesem Wert entsprechen, in einer Kategorie zusammengefasst werden. Anschließend können Sie mit der 2x2-Tabelle die Kappa-Statistik berechnen.

Formeln

Wenn der tatsächliche Standard unbekannt ist, schätzt Minitab die Cohen-Kappa-Statistik wie folgt:

	Versuch B (oder Prüfer B)
Versuch A (oder Prüfer A)	1	2	...	k	Gesamt
1	p₁₁	p₁₂	...	p_1k	p₁₊
2	p₂₁	p₂₂	...	p_2k	P₂₊
....
k	p_k1	p_k2	...	p_kk	p_k+.
Gesamt	p_.+1	p_.+2	...	p_.+k	1

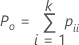
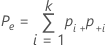
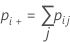
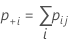
Notation

Begriff	Beschreibung
P_o	beobachteter Anteil der Übereinstimmungen
p_ii	jeder Wert in der Diagonalen der Zwei-Weg-Tabelle
P_e	erwarteter Anteil der Fälle, in denen die Bewertungen von k Prüfern übereinstimmen
n_ij	Anzahl der Stichproben in der i-ten Zeile und der j-ten Spalte
N	Gesamtzahl der Stichproben

Cohen-Kappa-Statistik (bekannter Standard)

Wenn die Klassifikationen nominal sind, verwenden Sie die Cohen-Kappa-Statistik. Wenn der Standard bekannt ist und Sie die Option zum Bestimmen der Cohen-Kappa-Statistik auswählen, berechnet Minitab die Statistik mit den unten stehenden Formeln.

Der Kappa-Koeffizient für die Übereinstimmung der Versuche mit dem bekannten Standard ist der Mittelwert dieser Kappa-Koeffizienten.

Formeln

Wenn der tatsächliche Standard bekannt ist, berechnen Sie zuerst Kappa unter Verwendung der Daten aus jedem Versuch und des bekannten Standards.

	Standard
Versuch A	1	2	...	k	Gesamt
1	p₁₁	p₁₂	...	p_1k	p₁₊
2	p₂₁	p₂₂	...	p_2k	P₂₊
....
k	p_k1	p_k2	...	p_kk	p_k+.
Gesamt	p_.+1	p_.+2	...	p_.+k	1

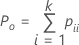
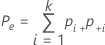
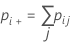
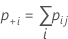
Notation

Begriff	Beschreibung
P_o	beobachteter Anteil der Übereinstimmung
p_ii	jeder Wert in der Diagonalen der Zwei-Weg-Tabelle
P_e	erwarteter Anteil der Fälle, in denen die Bewertungen von k Prüfern übereinstimmen
n_ij	Anzahl der Stichproben in der i-ten Zeile und der j-ten Spalte
N	Gesamtzahl der Stichproben

Testen der Signifikanz des Cohen-Kappa

Verwenden Sie Folgendes zum Testen der Nullhypothese, dass die Einstufungen unabhängig sind (so dass Kappa = 0):

z = Kappa / SE von Kappa

Dies ist ein einseitiger Test. Unter der Nullhypothese folgt z der Standardnormalverteilung. Weisen Sie die Hypothese zurück, wenn z signifikant größer als der kritische α-Wert ist.

Formeln

Der Standardfehler von Kappa für jeden Versuch und den Standard ist:

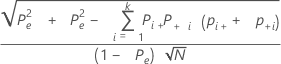
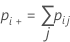
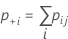
Notation

Begriff	Beschreibung
P_e	erwarteter Anteil der Fälle, in denen die Bewertungen von k Prüfern übereinstimmen
N	Gesamtzahl der Stichproben

Fleiss-Kappa-Statistik (unbekannter Standard)

Es gibt zwei Fälle, in denen die Kappa-Statistik berechnet wird.

Fall 1: Übereinstimmung innerhalb jedes Prüfers: Es werden die Kappa-Koeffizienten berechnet, die die Übereinstimmung innerhalb jedes Prüfers darstellen.; In diesem Fall ist m = die Anzahl der Versuche innerhalb jedes Prüfers, und es wird angenommen, dass m >1. Der Analyst möchte die Übereinstimmung zwischen den m Versuchen innerhalb jedes Prüfers untersuchen. Hierbei wird angenommen, dass jeder Versuch unter der Bedingung durchgeführt wird, dass dem Prüfer die Einstufungen aus früheren Versuchen nicht mehr bekannt sind.
Fall 2: Übereinstimmung zwischen allen Prüfern: Es werden die Kappa-Koeffizienten berechnet, die die Übereinstimmung zwischen allen Prüfern darstellen.; In diesem Fall ist m = die Gesamtzahl der Versuche für alle Prüfer. Es wird angenommen, dass die Anzahl der Prüfer >1 ist, und die Anzahl der Versuche kann gleich 1 oder >1 sein. Der Analyst möchte die Übereinstimmung aller Prüfer untersuchen.

Formeln für Gesamt-Kappa

Sei x_ij die Anzahl der Einstufungen von Stichprobe i in Kategorie j, wobei i im Bereich von 1 bis n und j im Bereich von 1 bis k liegt.

Der Gesamt-Kappa-Koeffizient ist wie folgt definiert:

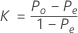
Dabei gilt Folgendes:

P_o ist der beobachtete Anteil der paarweisen Übereinstimmungen bei den m Versuchen.

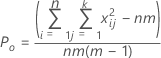
P_e ist der erwartete Anteil der Übereinstimmungen, wenn die Einstufungen aus einem Versuch unabhängig von den anderen sind.

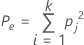
p_j stellt den Gesamtanteil der Einstufungen in Kategorie j dar.

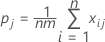
Wenn P_o und P_e in K eingesetzt werden, wird der Gesamt-Kappa-Koeffizient wie folgt geschätzt:

Dabei gilt Folgendes:

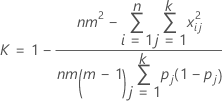
Begriff	Beschreibung
k	Gesamtzahl der Kategorien
m	Anzahl der Versuche; für Fall 1 ist m = die Anzahl der Versuche für jeden Prüfer; für Fall 2 ist m = die Anzahl der Versuche für alle Prüfer.
n	Anzahl der Stichproben
x_ij	Anzahl der Einstufungen von Stichprobe i in Kategorie j

Formeln für Kappa für eine einzelne Kategorie

Zum Messen der Übereinstimmung in Bezug auf die Einstufung in eine einzelne der k Kategorien, z. B. die j-te Kategorie, können alle übrigen Kategorien in einer einzigen Kategorie zusammengefasst werden; anschließend wird die obige Gleichung angewendet. Die resultierende Formel für die Kappa-Statistik der j-ten Kategorie lautet wie folgt:

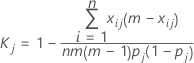
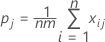
Dabei gilt Folgendes:

Begriff	Beschreibung
k	Gesamtzahl der Kategorien
m	Anzahl der Versuche; für Fall 1 ist m = die Anzahl der Versuche für jeden Prüfer; für Fall 2 ist m = die Anzahl der Versuche für alle Prüfer.
n	Anzahl der Stichproben
x_ij	Anzahl der Einstufungen von Stichprobe i in Kategorie j

Testen der Signifikanz des Fleiss-Kappa (unbekannter Standard)

Die Nullhypothese H₀ lautet, dass Kappa = 0. Die Alternativhypothese H₁ lautet, dass Kappa > 0.

Unter der Nullhypothese ist z annähernd normalverteilt und wird zum Berechnen der p-Werte verwendet.

Formeln

Verwenden Sie die folgende z-Statistik, um zu testen, ob Kappa > 0:

Var (K) wird wie folgt berechnet:

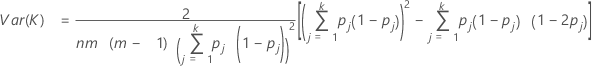
Verwenden Sie die folgende z-Statistik, um zu testen, ob Kappa > 0 für die j-te Kategorie:

Var (K_j) wird wie folgt berechnet:

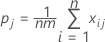
Notation

Begriff	Beschreibung
K	Gesamt-Kappa-Statistik
K_j	Kappa-Statistik für die j-te Kategorie
k	Gesamtzahl der Kategorien
m	Anzahl der Versuche; für Fall 1 ist m = die Anzahl der Versuche für jeden Prüfer; für Fall 2 ist m = die Anzahl der Versuche für alle Prüfer.
n	Anzahl der Stichproben
x_ij	Anzahl der Einstufungen von Stichprobe i in Kategorie j

Fleiss-Kappa-Statistik (bekannter Standard)

Führen Sie die folgenden Schritte aus, um das Gesamt-Kappa und das Kappa für eine bestimmte Kategorie zu berechnen, wenn die Standardeinstufung jeder Stichprobe bekannt ist.

Angenommen, es wurden m Versuche durchgeführt.

Hinweis

Ziehen Sie die Formeln der Fleiss-Kappa-Statistik (unbekannter Standard) heran.

Berechnen Sie für jeden Versuch den Kappa-Wert unter Verwendung der Einstufungen aus dem Versuch und der durch den Standard vorgegebenen Einstufungen. Mit anderen Worten: Behandeln Sie den Standard als einen weiteren Versuch, und verwenden Sie die Kappa-Formeln für den unbekannten Standard für zwei Versuche, um die Kappa-Statistik zu schätzen.
Wiederholen Sie diese Berechnung für alle m Versuche.
Nun verfügen Sie über m Gesamt-Kappa-Werte und m Kappa-Werte für die spezifischen Kategoriewerte.

Das Gesamt-Kappa bei bekanntem Standard entspricht dann dem Durchschnitt aller m Gesamt-Kappa-Werte.

Ebenso ist das Kappa für eine bestimmte Kategorie mit bekanntem Standard der Durchschnitt aller m Kappa-Statistiken für bestimmte Kategoriewerte.

Testen der Signifikanz des Fleiss-Kappa (bekannter Standard)

Die Nullhypothese H₀ lautet, dass Kappa = 0. Die Alternativhypothese H₁ lautet, dass Kappa > 0.

Laut der Nullhypothese ist z annähernd normalverteilt und wird zum Berechnen der p-Werte verwendet.

Hierbei ist K die Kappa-Statistik, und Var(K) ist die Varianz der Kappa-Statistik.

Hinweis

Ziehen Sie die Formeln der Fleiss-Kappa-Statistik (unbekannter Standard) heran.

Angenommen, es wurden m Versuche durchgeführt.

Berechnen Sie für jeden Versuch die Varianz von Kappa unter Verwendung der Einstufungen aus dem Versuch und der durch den Standard vorgegebenen Einstufungen. Mit anderen Worten: Behandeln Sie den Standard als zweiten Versuch, und berechnen Sie die Varianz mit den Formeln für die Varianz der Kappa-Statistik für den Fall mit zwei Versuchen und unbekanntem Standard.
Wiederholen Sie diese Berechnung für alle m Versuche.
Nun verfügen Sie über m Varianzen für die Gesamt-Kappa-Statistik und über m Varianzen für die Kappa-Statistik für spezifische Kategorien.

Die Varianz des Gesamt-Kappa mit bekannten Standards ist dann gleich der Summe der m Varianzen für das Gesamt-Kappa dividiert durch m².

Ebenso ist die Varianz des Kappa für eine spezifische Kategorie mit bekanntem Standard gleich der Summe der m Varianzen für das Kappa einer spezifischen Kategorie dividiert durch m².