Support für Minitab® 

Beispiel für Prüferübereinstimmung bei attributiven Daten

Weitere Informationen zu Minitab

Stoffprüfer in einem Textildruckunternehmen bewerten die Druckqualität für Baumwollstoffe auf einer Skala von 1 bis 5 Punkten. Der Qualitätstechniker möchte die Beständigkeit und Richtigkeit der Bewertungen der Prüfer untersuchen. Der Techniker fordert vier Prüfer auf, die Druckqualität von 50 Stoffstichproben in zufälliger Reihenfolge zweimal zu bewerten.

Da die Daten einen bekannten Standard für jede Stichprobe enthalten, kann der Qualitätstechniker die Beständigkeit und Richtigkeit der Bewertungen in Bezug auf den Standard sowie im Vergleich mit anderen Prüfern beurteilen.

  1. Öffnen Sie die Beispieldaten Textildruckqualität.MWX.
  2. Wählen Sie Statistik > Qualitätswerkzeuge > Prüferübereinstimmung bei attributiven Daten aus.
  3. Wählen Sie im Feld Anordnung der Daten die Option Attributspalte aus, und geben Sie Antwort ein.
  4. Geben Sie im Feld Stichproben die Spalte Stichprobe ein.
  5. Geben Sie im Feld Prüfer die Spalte Prüfer ein.
  6. Geben Sie im Feld Bekannter Standard/Attribut die Spalte Standard ein.
  7. Wählen Sie Kategorien der Attributdaten sind geordnet aus.
  8. Klicken Sie auf OK.

Interpretieren der Ergebnisse

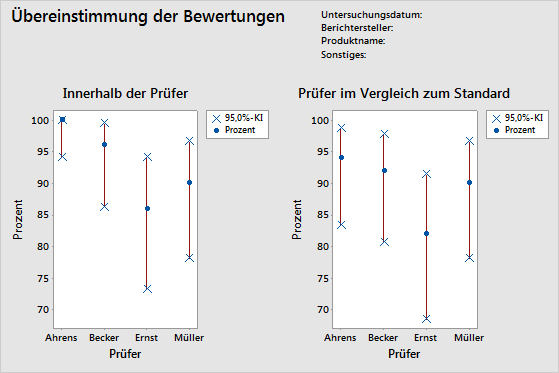
Tabelle „Innerhalb der Prüfer“
Da jeder Prüfer mindestens zwei Einstufungen für jede Stichprobe abgibt, kann der Techniker die Beständigkeit jedes Prüfers auswerten.
Alle Prüfer weisen gute Übereinstimmungsraten auf, von Ahrens mit 100 % bis hin zu Ernst mit 86 %.
Der p-Wert für die Fleiss-Kappa-Statistik beträgt für alle Prüfer und alle Werte der Antwortvariablen 0,0000 bei α = 0,05. Daher weist der Techniker die Nullhypothese zurück, dass die Übereinstimmungen ausschließlich auf Zufall zurückzuführen sind.
Da die Einstufungen in diesem Beispiel ordinal sind, untersucht der Techniker den Kendall-Koeffizienten der Konkordanz. Der Kendall-Koeffizient der Konkordanz für alle Prüfer liegt zwischen 0,98446 und 1,000. Dies verweist auf ein hohes Maß an Übereinstimmung.
Tabelle „Jeder Prüfer im Vergleich zum Standard“
Da ein bekannter Standard für jede Stichprobe vorliegt, kann der Techniker die Genauigkeit und Beständigkeit der Einstufungen eines bestimmten Prüfers bewerten.
Jeder Prüfer hat 50 Stoffstichproben eingestuft (# Geprüft). Ahrens hat 47 Stichproben versuchsübergreifend richtig eingestuft (# Übereinstimmungen) und somit 94 % Übereinstimmungen erzielt. Ernst hat versuchsübergreifend mit 82 % Übereinstimmungen 41 Stichproben richtig beurteilt.
Der p-Wert für Fleiss-Kappa beträgt für alle Prüfer und alle werte der Antwortvariablen 0,0000 bei α = 0,05. Daher weist der Techniker die Nullhypothese zurück, dass die Übereinstimmungen ausschließlich auf Zufall zurückzuführen sind.
Der Kendall-Koeffizient der Korrelation für alle Prüfer liegt zwischen 0,951863 und 0,975168, wodurch das hohe Maß an Übereinstimmung mit dem Standard bestätigt wird.
Tabelle „Zwischen Prüfern“
In der Tabelle „Zwischen Prüfern“ wird verdeutlicht, dass die Prüfer bei 37 der 50 Stichproben in ihren Einstufungen übereinstimmen.
Der Kappa-Gesamtwert von 0,881705 zeigt ein gutes Maß an absoluter Übereinstimmung der Einstufungen zwischen den Prüfern. Der Kendall-Koeffizient der Konkordanz 0,976681 bestätigt diese starke Assoziation.
In der Statistik zwischen den Prüfern werden die Einstufungen der Prüfer nicht mit dem bekannten Standard verglichen. Diese Statistiken geben an, ob die Einstufungen der Prüfer beständig, jedoch nicht, ob sie richtig sind.
Tabelle „Alle Prüfer im Vergleich zum Standard“
Da ein bekannter Standard für jede Stichprobe vorliegt, kann der Techniker die Genauigkeit der Einstufungen aller Prüfer bewerten.
Bei den Einstufungen aller Prüfer stimmten 37 von 50 Einstufungen mit dem bekannten Standard überein. Dies entspricht einer Übereinstimmungsquote von 74,0 %.
Der Kappa-Gesamtwert von 0,912082 zeigt ein gutes Maß an absoluter Übereinstimmung der Einstufungen zwischen den Prüfern und mit dem Standard. Der Kendall-Koeffizient der Konkordanz 0,965563 bestätigt diese starke Assoziation.
In der Statistik „Alle Prüfer im Vergleich zum Standard“ werden die Einstufungen durch die Prüfer mit dem Standard verglichen. Der Techniker kann die Schlussfolgerung ziehen, dass die Einstufungen der Prüfer beständig und richtig sind.
Hinweis

Der p-Wert von 0,0000 in der Ausgabe ist gerundet. Sie können jedoch mit Sicherheit folgern, dass der p-Wert sehr klein und < 0,00005 ist.

Übereinstimmung der Bewertungen

Prüfer# Geprüft# ÜbereinstimmungenProzent95%-KI
Ahrens5050100,00(94,18; 100,00)
Becker504896,00(86,29; 99,51)
Ernst504386,00(73,26; 94,18)
Müller504590,00(78,19; 96,67)
# Übereinstimmungen: Der Prüfer stimmt versuchsübergreifend mit sich selbst überein.

Fleiss-Kappa-Statistik

PrüferAntwortKappaSE KappazP(vs > 0)
Ahrens11,000000,1414217,07110,0000
  21,000000,1414217,07110,0000
  31,000000,1414217,07110,0000
  41,000000,1414217,07110,0000
  51,000000,1414217,07110,0000
  Gesamt1,000000,07105214,07410,0000
Becker11,000000,1414217,07110,0000
  20,896050,1414216,33600,0000
  30,864500,1414216,11290,0000
  41,000000,1414217,07110,0000
  51,000000,1414217,07110,0000
  Gesamt0,949650,07140113,30020,0000
Ernst10,830600,1414215,87330,0000
  20,840000,1414215,93970,0000
  30,702380,1414214,96660,0000
  40,702380,1414214,96660,0000
  51,000000,1414217,07110,0000
  Gesamt0,823540,07159111,50340,0000
Müller11,000000,1414217,07110,0000
  20,830600,1414215,87330,0000
  30,819170,1414215,79240,0000
  40,864500,1414216,11290,0000
  50,864500,1414216,11290,0000
  Gesamt0,874720,07094512,32950,0000

Kendall-Koeffizient der Konkordanz

PrüferKoefChi-QdDFp
Ahrens1,0000098,0000490,0000
Becker0,9944897,4587490,0000
Ernst0,9844696,4769490,0001
Müller0,9870096,7256490,0001

Übereinstimmung der Bewertungen

Prüfer# Geprüft# ÜbereinstimmungenProzent95%-KI
Ahrens504794,00(83,45; 98,75)
Becker504692,00(80,77; 97,78)
Ernst504182,00(68,56; 91,42)
Müller504590,00(78,19; 96,67)
# Übereinstimmungen: Die Bewertungen des Prüfers stimmen versuchsübergreifend mit dem
     bekannten Standard überein.

Fleiss-Kappa-Statistik

PrüferAntwortKappaSE KappazP(vs > 0)
Ahrens11,000000,10000010,00000,0000
  20,830600,1000008,30600,0000
  30,819170,1000008,19170,0000
  41,000000,10000010,00000,0000
  51,000000,10000010,00000,0000
  Gesamt0,924760,05025718,40060,0000
Becker11,000000,10000010,00000,0000
  20,838380,1000008,38380,0000
  30,807250,1000008,07250,0000
  41,000000,10000010,00000,0000
  51,000000,10000010,00000,0000
  Gesamt0,924620,05039618,34730,0000
Ernst10,911590,1000009,11590,0000
  20,810350,1000008,10350,0000
  30,726190,1000007,26190,0000
  40,849190,1000008,49190,0000
  51,000000,10000010,00000,0000
  Gesamt0,861630,05050017,06220,0000
Müller11,000000,10000010,00000,0000
  20,916940,1000009,16940,0000
  30,907360,1000009,07360,0000
  40,929130,1000009,29130,0000
  50,935020,1000009,35020,0000
  Gesamt0,937320,05021118,66740,0000

Kendall-Korrelationskoeffizient

PrüferKoefSE Koefzp
Ahrens0,9673860,069006614,01280,0000
Becker0,9678350,069006614,01930,0000
Ernst0,9518630,069006613,78790,0000
Müller0,9751680,069006614,12560,0000

Übereinstimmung der Bewertungen

# Geprüft# ÜbereinstimmungenProzent95%-KI
503774,00(59,66; 85,37)
# Übereinstimmungen: Die Bewertungen aller Prüfer stimmen miteinander überein.

Fleiss-Kappa-Statistik

AntwortKappaSE KappazP(vs > 0)
10,9543920,026726135,71010,0000
20,8276940,026726130,96950,0000
30,7725410,026726128,90580,0000
40,8911270,026726133,34290,0000
50,9681480,026726136,22480,0000
Gesamt0,8817050,013436265,62180,0000

Kendall-Koeffizient der Konkordanz

KoefChi-QdDFp
0,976681382,859490,0000

Übereinstimmung der Bewertungen

# Geprüft# ÜbereinstimmungenProzent95%-KI
503774,00(59,66; 85,37)
# Übereinstimmungen: Die Bewertungen aller Prüfer stimmen mit dem bekannten Standard überein.

Fleiss-Kappa-Statistik

AntwortKappaSE KappazP(vs > 0)
10,9778970,050000019,55790,0000
20,8490680,050000016,98140,0000
30,8149920,050000016,29980,0000
40,9445800,050000018,89160,0000
50,9837560,050000019,67510,0000
Gesamt0,9120820,025170536,23620,0000

Kendall-Korrelationskoeffizient

KoefSE Koefzp
0,9655630,034503327,98170,0000

Copyright © 2025 Minitab, LLC. All rights Reserved.