Wenn sich Ihre Daten durch Überdispersion oder Unterdispersion auszeichnen, kann mit Hilfe einer Regelkarte für attributive Daten nach Laney (eine p′-Karte nach Laney oder eine u′-Karte nach Laney) möglicherweise genauer zwischen Streuung durch gewöhnliche Ursachen und Streuung durch Ausnahmebedingungen unterschieden werden als mit einer herkömmlichen Regelkarte für attributive Daten (z. B. einer p-Karte oder einer u-Karte). Die Berechnungen für die Regelkarten für attributive Daten nach Laney umfassen Sigma-Z, eine Korrektur für die Über- bzw. Unterdispersion. Ein Sigma-Z von 1 gibt an, dass keine Korrektur erforderlich ist und die Regelkarte für attributive Daten nach Laney exakt einer herkömmlichen Regelkarte für attributive Daten entspricht.
Um eine p'-Karte nach Laney zu erstellen, wählen Sie aus. Um eine u'-Karte nach Laney zu erstellen, wählen Sie aus.
Was ist Überdispersion?
Überdispersion liegt vor, wenn die Daten eine größere Streuung aufweisen als nach einer Binomialverteilung (für fehlerhafte Einheiten) oder einer Poisson-Verteilung (für Fehler) zu erwarten wäre. Bei herkömmlichen p-Karten und u-Karten wird angenommen, dass die Rate der fehlerhaften Einheiten oder Fehler im Lauf der Zeit konstant bleibt. Externe Rauschfaktoren, bei denen es sich nicht um Ausnahmebedingungen handelt, verursachen jedoch normalerweise einen gewissen Grad der Streuung in der Rate der fehlerhaften Einheiten oder Fehler über einen Zeitraum.
Die Eingriffsgrenzen auf einer herkömmlichen p-Karte oder u-Karte werden bei größeren Teilgruppen schmaler. Wenn die Teilgruppen ausreichend groß sind, kann die Überdispersion bewirken, dass Punkte scheinbar außer Kontrolle sind, während dies tatsächlich nicht zutrifft. Bei der Regelkarte für attributive Daten nach Laney beinhaltet die Definition der Streuung durch gewöhnliche Ursachen nicht nur die Streuung innerhalb der Teilgruppen, sondern auch die durchschnittliche Streuung zwischen aufeinander folgenden Teilgruppen. Bei einer Überdispersion sind die Eingriffsgrenzen auf einer Regelkarte für attributive Daten nach Laney breiter als auf einer herkömmlichen Regelkarte für attributive Daten.
Die Beziehung zwischen Teilgruppengröße und den Eingriffsgrenzen auf einer herkömmlichen Regelkarte für attributive Daten ähnelt der zwischen der Trennschärfe und einem t-Test bei einer Stichprobe. Bei größeren Stichproben weist der t-Test eine größere Trennschärfe zum Erkennen einer Differenz auf. Wenn die Stichprobe jedoch ausreichend groß ist, kann selbst eine äußerst kleine, an sich belanglose Differenz statistisch signifikant werden. Bei einer Stichprobe von 1.000.000 Beobachtungen könnte ein t-Test beispielsweise feststellen, dass sich ein Stichprobenmittelwert von 50,001 signifikant von 50 unterscheidet. Eine Differenz von 0,001 hat jedoch u. U. keine praktischen Konsequenzen für Ihren Prozess.
Was ist Unterdispersion?
Unterdispersion ist das Gegenteil der Überdispersion. Unterdispersion liegt vor, wenn die Daten eine geringere Streuung aufweisen als nach einer Binomialverteilung (für fehlerhafte Einheiten) oder einer Poisson-Verteilung (für Fehler) zu erwarten wäre. Unterdispersion kann auftreten, wenn benachbarte Teilgruppen miteinander korrelieren (dies wird auch als Autokorrelation bezeichnet).
Wenn Daten eine Unterdispersion aufweisen, liegen die Eingriffsgrenzen auf einer herkömmlichen p- oder u-Karte u. U. zu weit auseinander. Bei zu weiten Eingriffsgrenzen ist es möglich, dass Sie Streuung durch Ausnahmebedingungen übersehen und für Streuung durch gewöhnliche Ursachen halten. Bei einer Unterdispersion sind die Eingriffsgrenzen auf einer Regelkarte für attributive Daten nach Laney enger als auf einer herkömmlichen Regelkarte für attributive Daten.
Wenn beispielsweise ein Werkzeug verschleißt, kann sich die Anzahl der Fehler erhöhen. Durch den Anstieg der Fehleranzahl in den Teilgruppen können die Teilgruppen untereinander ähnlicher werden, als sie es rein zufällig wären.
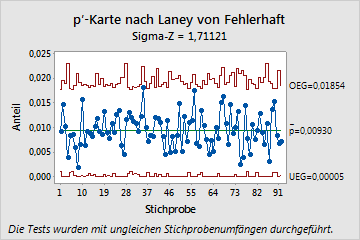
Vergleich zwischen herkömmlichen Regelkarten für attributive Daten und Regelkarten für attributive Daten nach Laney
Die folgenden Grafiken zeigen eine herkömmliche p-Karte und eine p'-Karte nach Laney derselben Daten. Diese Daten werden auch im Beispiel für die p'-Karte nach Laney und im Beispiel für die p-Karten-Diagnose dargestellt. Die Teilgruppen sind mit durchschnittlich jeweils ungefähr 2500 Beobachtungen sehr groß. Außerdem ergibt die p-Karten-Diagnose eine Überdispersion der Daten.
Auf der herkömmlichen p-Karte führen die großen Teilgruppengrößen zu sehr engen Eingriffsgrenzen. Bei den engen Eingriffsgrenzen führt die Überdispersion dazu, dass mehrere Teilgruppen anscheinend außer Kontrolle sind. Die p'-Karte nach Laney korrigiert jedoch die Überdispersion und zeigt, dass der Prozess tatsächlich beherrscht ist. Keine Punkte liegen außerhalb der Eingriffsgrenzen.
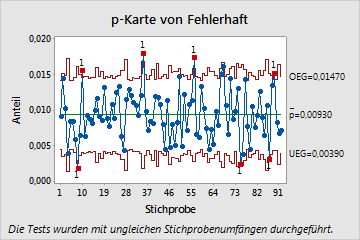
Herkömmliche p-Karte