Die Prozessstandardabweichung wird auch als Sigma oder σ bezeichnet. Wenn Sie einen historischen Wert für Sigma angeben, verwendet Minitab den historischen Wert. Wenn Sie keinen Wert eingeben, verwendet Minitab eine der folgenden Methoden, um Sigma aus den Daten zu schätzen.
In diesem Thema
S-quer-Methode
Ohne Konstante für erwartungstreue Schätzung
Wenn Sie keine Konstante für die erwartungstreue Schätzung verwenden, ist S-quer der Mittelwert der Teilgruppenstandardabweichungen:
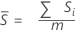
Mit Konstante für erwartungstreue Schätzung
Wenn Sie die Konstante für die erwartungstreue Schätzung c4(ni) verwenden, wird S-quer wie folgt berechnet:
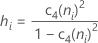
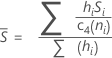
Wenn die Teilgruppengröße konstant ist, ist S-quer:
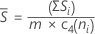
Notation
| Begriff | Beschreibung |
|---|---|
| c4 (ni) | Wert der Konstanten für erwartungstreue Schätzung c4, der dem in Klammern angegebenen Wert entspricht. |
| Si | Standardabweichung von Teilgruppe i |
| m | Anzahl der Teilgruppen |
Methode der zusammengefassten Standardabweichung
Die zusammengefasste Standardabweichung (Sp) wird mit der folgenden Formel berechnet:
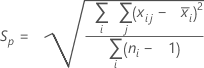
Wenn die Teilgruppengröße konstant ist, kann Sp auch wie folgt berechnet werden:

Mit Konstante für erwartungstreue Schätzung
Standardmäßig wendet Minitab die Konstante für die erwartungstreue Schätzung c4() an, wenn Sie die zusammengefasste Standardabweichung zum Schätzen von σ verwenden:


Notation
| Begriff | Beschreibung |
|---|---|
| xij | j-te Beobachtung in der i-ten Teilgruppe |
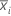 | Mittelwert der Teilgruppe i |
| ni | Anzahl der Beobachtungen in Teilgruppe i |
| μv | Mittelwert der Varianzen der Teilgruppen |
| c4(·) | Wert der Konstanten für erwartungstreue Schätzung c4, der dem in Klammern angegebenen Wert entspricht. |
| d | Freiheitsgrade für Sp, durch die folgende Formel angegeben:
 |
Konstanten für erwartungstreue Schätzung c4() und c5()
c4()

c5()

Notation
| Begriff | Beschreibung |
|---|---|
| Γ() | Gamma-Funktion |
