Die Prozessstandardabweichung wird auch als Sigma oder σ bezeichnet. Wenn Sie einen historischen Wert für Sigma angeben, verwendet Minitab den historischen Wert. Andernfalls verwendet Minitab eine der folgenden Methoden, um Sigma aus den Daten zu schätzen.
In diesem Thema
R-quer-Methode
Minitab verwendet die Spannweite jeder Teilgruppe, 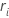 , zum Berechnen von
, zum Berechnen von 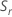 , einem erwartungstreuen Schätzwert von σ:
, einem erwartungstreuen Schätzwert von σ:
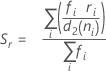
Dabei gilt Folgendes:
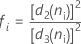
Wenn die Teilgruppengröße konstant ist, vereinfacht sich die Formel wie folgt:
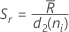
wobei 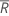 (R-quer) der Mittelwert der Teilgruppenspannweiten ist, der wie folgt berechnet wird:
(R-quer) der Mittelwert der Teilgruppenspannweiten ist, der wie folgt berechnet wird:

Notation
| Begriff | Beschreibung |
|---|---|
| ri | Spannweite für Teilgruppe i |
| m | Anzahl der Teilgruppen |
| d2(·) | Wert der Konstanten für erwartungstreue Schätzung d2, der dem in Klammern angegebenen Wert entspricht |
| ni | Anzahl der Beobachtungen in Teilgruppe i |
| d3(·) | Wert der Konstanten für erwartungstreue Schätzung d3, der dem in Klammern angegebenen Wert entspricht |
Methode der zusammengefassten Standardabweichung
Die zusammengefasste Standardabweichung (Sp) wird mit der folgenden Formel berechnet:
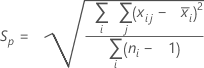
Wenn die Teilgruppengröße konstant ist, kann Sp auch wie folgt berechnet werden:

Mit Konstante für erwartungstreue Schätzung
Standardmäßig wendet Minitab die Konstante für die erwartungstreue Schätzung c4() an, wenn Sie die zusammengefasste Standardabweichung zum Schätzen von σ verwenden:


Notation
| Begriff | Beschreibung |
|---|---|
| xij | j-te Beobachtung in der i-ten Teilgruppe |
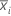 | Mittelwert der Teilgruppe i |
| ni | Anzahl der Beobachtungen in Teilgruppe i |
| μv | Mittelwert der Varianzen der Teilgruppen |
| c4(·) | Wert der Konstanten für erwartungstreue Schätzung c4, der dem in Klammern angegebenen Wert entspricht. |
| d | Freiheitsgrade für Sp, durch die folgende Formel angegeben:
 |
Konstanten für erwartungstreue Schätzung d2(), d3() und d4()
d2(N) ist der erwartete Wert der Spannweite von N Beobachtungen aus einer normalverteilten Grundgesamtheit mit Standardabweichung = 1. Wenn also r die Spannweite einer Stichprobe von N Beobachtungen aus einer Normalverteilung mit Standardabweichung = σ ist, dann ist E(r) = d2(N)σ.
d3(N) ist die Standardabweichung der Spannweite von N Beobachtungen aus einer normalverteilten Grundgesamtheit mit σ = 1. Wenn also r die Spannweite einer Stichprobe von N Beobachtungen aus einer Normalverteilung mit Standardabweichung = σ ist, dann ist StdAbw(r) = d3(N)σ.
Suchen Sie in der folgenden Tabelle eine Konstante für die erwartungstreue Schätzung für einen bestimmten Wert N. (Ziehen Sie zum Bestimmen des Werts von N die Formel für die betreffende Statistik hinzu.)

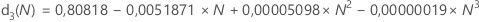

- D. J. Wheeler und D. S. Chambers. (1992). Understanding Statistical Process Control, Second Edition, SPC Press, Inc.
- H. Leon Harter (1960). „Tables of Range and Studentized Range“. The Annals of Mathematical Statistics, Vol. 31, Nr. 4, Institute of Mathematical Statistics, S. 1122−1147.
| N | d2(N) | d3(N) | d4(N) |
|---|---|---|---|
| 2 | 1,128 | 0,8525 | 0,954 |
| 3 | 1,693 | 0,8884 | 1,588 |
| 4 | 2,059 | 0,8798 | 1,978 |
| 5 | 2,326 | 0,8641 | 2,257 |
| 6 | 2,534 | 0,848 | 2,472 |
| 7 | 2,704 | 0,8332 | 2,645 |
| 8 | 2,847 | 0,8198 | 2,791 |
| 9 | 2,970 | 0,8078 | 2,915 |
| 10 | 3,078 | 0,7971 | 3,024 |
| 11 | 3,173 | 0,7873 | 3,121 |
| 12 | 3,258 | 0,7785 | 3,207 |
| 13 | 3,336 | 0,7704 | 3,285 |
| 14 | 3,407 | 0,7630 | 3,356 |
| 15 | 3,472 | 0,7562 | 3,422 |
| 16 | 3,532 | 0,7499 | 3,482 |
| 17 | 3,588 | 0,7441 | 3,538 |
| 18 | 3,640 | 0,7386 | 3,591 |
| 19 | 3,689 | 0,7335 | 3,640 |
| 20 | 3,735 | 0,7287 | 3,686 |
| 21 | 3,778 | 0,7242 | 3,730 |
| 22 | 3,819 | 0,7199 | 3,771 |
| 23 | 3,858 | 0,7159 | 3,811 |
| 24 | 3,895 | 0,7121 | 3,847 |
| 25 | 3,931 | 0,7084 | 3,883 |
| N | d2(N) |
|---|---|
| 26 | 3,964 |
| 27 | 3,997 |
| 28 | 4,027 |
| 29 | 4,057 |
| 30 | 4,086 |
| 31 | 4,113 |
| 32 | 4,139 |
| 33 | 4,165 |
| 34 | 4,189 |
| 35 | 4,213 |
| 36 | 4,236 |
| 37 | 4,259 |
| 38 | 4,280 |
| 39 | 4,301 |
| 40 | 4,322 |
| 41 | 4,341 |
| 42 | 4,361 |
| 43 | 4,379 |
| 44 | 4,398 |
| 45 | 4,415 |
| 46 | 4,433 |
| 47 | 4,450 |
| 48 | 4,466 |
| 49 | 4,482 |
| 50 | 4,498 |
Konstanten für erwartungstreue Schätzung c4() und c5()
c4()

c5()

Notation
| Begriff | Beschreibung |
|---|---|
| Γ() | Gamma-Funktion |
