In diesem Thema
Zusätzliche σ-Grenzen anzeigen bei
Geben Sie im Feld Diesen Vielfachen der Standardabweichung einen oder mehrere Werte für die Anzeige zusätzlicher Standardabweichungslinien auf der Regelkarte ein.
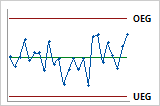
Standardmäßige 3-Sigma-Grenzen
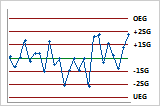
Zusätzliche Sigma-Grenzen bei 1 und 2 Standardabweichungen
Eingriffsgrenzen einschränken
Sie können für die Eingriffsgrenzen eine Untergrenze und eine Obergrenze angeben. Wenn die berechnete Eingriffsgrenze weiter als der angegebene Wert von der Mittellinie liegt, zeigt Minitab anstelle der Eingriffsgrenze eine Begrenzung an. Minitab beschriftet die Untergrenze mit UG und die Obergrenze mit OG.
Hinweis
Obergrenzen und Untergrenzen haben keine Einfluss auf die Berechnungen für die Tests auf Ausnahmebedingungen.
Erzwingen, dass die Eingriffsgrenzen Geraden sind
Standardmäßig berechnet Minitab die Eingriffsgrenzen anhand der tatsächlichen Teilgruppengrößen. Wenn die Teilgruppengrößen unterschiedlich sind, sind die Eingriffsgrenzen ungleichmäßig. Sie können aber erzwingen, dass die Eingriffsgrenzen Geraden sind. Wählen Sie unter Bei ungleichen Teilgruppengrößen Eingriffsgrenzen berechnen die Option Angenommene Größe für alle Teilgruppen aus, und geben Sie eine Teilgruppengröße ein.
Diese Option ist insbesondere dann nützlich, wenn alle Teilgruppen zwar dieselbe Größe haben sollten, einige Teilgruppen aber eine andere Größe aufweisen. Einige Teilgruppen sind zum Beispiel aufgrund fehlender Messungen kleiner. Legen Sie die Teilgruppengröße in diesem Fall auf die vorgesehene Größe fest.
Wenn bei der Regelkarte der gleitenden Durchschnitte konstante Teilgruppen angenommen werden, sind die resultierenden Grenzen nicht tatsächlich konstant. Wenn ein gleitender Durchschnitt der Länge K vorliegt, unterscheiden sich die Eingriffsgrenzen für die ersten K – 1 gleitenden Durchschnitte; dies ist auf die unterschiedliche Anzahl von Datenwerten zurückzuführen, die in den jeweiligen Werten für die ersten K −1 gleitenden Durchschnitte verwendet werden. Nach dem k-ten gleitenden Durchschnitt erhalten Sie konstante Grenzen.
Achtung
Wenn Sie eine Teilgruppengröße angeben, ändern Sie damit die Berechnungen für die Eingriffsgrenzen. Hierdurch können sich die Ergebnisse der Tests auf Ausnahmebedingungen ändern. Verwenden Sie diese Option nur, wenn die Differenzen zwischen den Teilgruppengrößen klein sind. Verwenden Sie diese Option nicht, wenn die Differenz zwischen den Teilgruppengrößen größer als 25 % ist. Wenn die größte Teilgruppe zum Beispiel 10 Beobachtungen und die kleinste Teilgruppe 8 Beobachtungen enthält, beträgt die Differenz 20 % ((10 – 8)/10 = 0,2 = 20 %).
Die Daten für die folgenden Regelkarten sind zwar beispielsweise identisch, aber die Eingriffsgrenzen für die zweite Regelkarte wurden auf der Grundlage einer festen Teilgruppengröße berechnet.
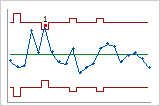
Tatsächliche Teilgruppengrößen