Sigma (σ) ist die Standardabweichung des Prozesses. Wenn Sie einen historischen Wert für σ eingeben, verwendet Minitab den historischen Wert. Andernfalls verwendet Minitab eine der folgenden Methoden, um σ aus den Daten zu schätzen.
In diesem Thema
Methode: Mittelwert der gleitenden Spannweite
Der Mittelwert der gleitenden Spannweite, 
, mit der Länge w wird mit der folgenden Formel angegeben:
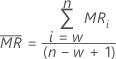
wobei MRi die gleitende Spannweite für Beobachtung i darstellt, die wie folgt berechnet wird:
Minitab verwendet 
zum Berechnen von Smr, einem erwartungstreuen Schätzwert von σ:
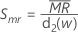
Notation
| Begriff | Beschreibung |
|---|---|
| n | Anzahl der Beobachtungen |
| w | Länge der gleitenden Spannweite. Der Standardwert ist 2. |
| d2() | Wert der Konstanten für erwartungstreue Schätzung d2, der dem in Klammern angegebenen Wert entspricht |
Methode: Median der gleitenden Spannweite
Der Median der gleitenden Spannweite, 
, mit der Länge w wird mit der folgenden Formel angegeben:
wobei MRi die gleitende Spannweite für Beobachtung i darstellt, die wie folgt berechnet wird:
Minitab verwendet 
zum Berechnen von Smr, einem erwartungstreuen Schätzwert von σ:
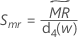
Notation
| Begriff | Beschreibung |
|---|---|
| n | Anzahl der Beobachtungen |
| w | Länge der gleitenden Spannweite. Der Standardwert ist 2. |
| d4() | Wert der Konstanten für erwartungstreue Schätzung d4, der dem in Klammern angegebenen Wert entspricht |
Methode: Quadratwurzel von MSSD
MSSD steht für das Mittel der quadrierten sukzessiven Differenzen. Die Quadratwurzel von MSSD (SRMSSD) wird wie folgt berechnet:
Mit Konstante für erwartungstreue Schätzung
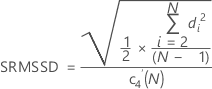
Ohne Konstante für erwartungstreue Schätzung
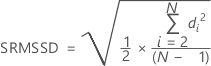
Notation
| Begriff | Beschreibung |
|---|---|
| di | Differenz zwischen dem Wert der Beobachtung i und dem Wert der Beobachtung i – 1 |
| N | Anzahl der Beobachtungen |
| c4'(N) | Konstante für erwartungstreue Schätzung aus einer Tabelle |
R-quer-Methode
Minitab verwendet die Spannweite jeder Teilgruppe,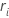 
, zum Berechnen von 
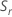, einem erwartungstreuen Schätzwert von σ:
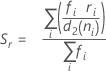
Dabei gilt Folgendes:
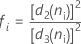
Wenn die Teilgruppengröße konstant ist, vereinfacht sich die Formel wie folgt:
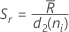
wobei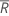 
(R-quer) der Mittelwert der Teilgruppenspannweiten ist, der wie folgt berechnet wird:
Notation
| Begriff | Beschreibung |
|---|---|
| ri | Spannweite für Teilgruppe i |
| m | Anzahl der Teilgruppen |
| d2(·) | Wert der Konstanten für erwartungstreue Schätzung d2, der dem in Klammern angegebenen Wert entspricht |
| ni | Anzahl der Beobachtungen in Teilgruppe i |
| d3(·) | Wert der Konstanten für erwartungstreue Schätzung d3, der dem in Klammern angegebenen Wert entspricht |
S-quer-Methode
Ohne Konstante für erwartungstreue Schätzung
Wenn Sie keine Konstante für die erwartungstreue Schätzung verwenden, ist S-quer der Mittelwert der Teilgruppenstandardabweichungen:
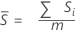
Mit Konstante für erwartungstreue Schätzung
Wenn Sie die Konstante für die erwartungstreue Schätzung c4(ni) verwenden, wird S-quer wie folgt berechnet:
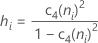
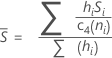
Wenn die Teilgruppengröße konstant ist, ist S-quer:
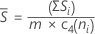
Notation
| Begriff | Beschreibung |
|---|---|
| c4 (ni) | Wert der Konstanten für erwartungstreue Schätzung c4, der dem in Klammern angegebenen Wert entspricht. |
| Si | Standardabweichung von Teilgruppe i |
| m | Anzahl der Teilgruppen |
Methode der zusammengefassten Standardabweichung
Die zusammengefasste Standardabweichung (Sp) wird mit der folgenden Formel berechnet:
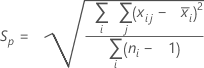
Wenn die Teilgruppengröße konstant ist, kann Sp auch wie folgt berechnet werden:
Mit Konstante für erwartungstreue Schätzung
Standardmäßig wendet Minitab die Konstante für die erwartungstreue Schätzung c4() an, wenn Sie die zusammengefasste Standardabweichung zum Schätzen von σ verwenden:
Notation
| Begriff | Beschreibung |
|---|---|
| xij | j-te Beobachtung in der i-ten Teilgruppe |
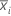 | Mittelwert der Teilgruppe i |
| ni | Anzahl der Beobachtungen in Teilgruppe i |
| μv | Mittelwert der Varianzen der Teilgruppen |
| c4(·) | Wert der Konstanten für erwartungstreue Schätzung c4, der dem in Klammern angegebenen Wert entspricht. |
| d | Freiheitsgrade für Sp, durch die folgende Formel angegeben:
 |
