Methoden und Formeln für g-Karte

Wählen Sie die gewünschte Methode oder Formel aus.

In diesem Thema

Dargestellte Punkte
Mittellinie und Eingriffsgrenzen
Tests auf Ausnahmebedingungen einschließlich des Benneyan-Tests

Dargestellte Punkte

Wenn die Daten als Datum jedes Ereignisses erfasst wurden, bildet jeder dargestellte Punkt x_i die Anzahl der Tage zwischen aufeinander folgenden Ereignissen ab. Wenn die Daten als Anzahl der Möglichkeiten zwischen Ereignissen erfasst wurden, bildet jeder dargestellte Punkt die Anzahl der Möglichkeiten zwischen aufeinander folgenden Ereignissen ab.

Mittellinie und Eingriffsgrenzen

Mittellinie

Die Mittellinie entspricht dem 50. Perzentil der Verteilung. Die Mittellinie ist gleich G2 – 1.

Hinweis

Es wird 1 subtrahiert, da Minitab in den Berechnungen die Definition „Anzahl bis zum Ereignis“ der geometrischen Verteilung verwendet, auf der g-Karte jedoch die Werte von „Anzahl zwischen Ereignissen“ dargestellt werden.

G2 ist gleich INVCDF (0,5) für eine geometrische Verteilung mit Parameter p.

Minitab liefert zwei Werte, G2_a und G2_b (G2_a = G2_b – 1), mit den zwei Wahrscheinlichkeiten p2_a und p2_b (p2_a < p2_b). Durch einfache lineare Interpolation ergibt sich G2 = G2_a + (0,5 – p2_a) / (p2_b – p2_a).

Untere Eingriffsgrenze (UEG)

UEG = G1 – 1

G1 ist gleich INVCDF (0,00135) für eine geometrische Verteilung mit Parameter p.

Minitab liefert zwei Werte, G1_a und G1_b (G1_a = G1_b – 1), mit den zwei Wahrscheinlichkeiten p1_a und p1_b (p1_a < p1_b). Durch einfache lineare Interpolation ergibt sich G1 = G1_a + (0,00135 – p1_a) / (p1_b – p1_a).

Obere Eingriffsgrenze (OEG)

OEG = G3 – 1

G3 ist gleich INVCDF (0,99865) für eine geometrische Verteilung mit Parameter p.

Minitab liefert zwei Werte, G3_a und G3_b (G3_a = G3_b – 1), mit den zwei Wahrscheinlichkeiten p3_a und p3_b (p3_a < p3_b). Durch einfache lineare Interpolation ergibt sich G3 = G3_a + (0,99865 – p3_a) / (p3_b – p3_a).

Notation

Begriff	Beschreibung
N	Anzahl der in den Berechnungen verwendeten Datenwerte. (Wenn Daten Datumsangaben sind, muss 1 subtrahiert werden, da Minitab die Differenzen darstellt.)
	Durchschnitt der dargestellten Punkte
Ereigniswahrscheinlichkeit (p)

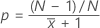Tests auf Ausnahmebedingungen einschließlich des Benneyan-Tests

Tests 1 bis 4

Test 1 basiert auf der geometrischen Verteilung. Tests 2, 3 und 4 sind identisch mit den Tests, die für Regelkarten für attributive Daten ausgeführt werden.

Wenn K = 3, definieren die Werte G1 und G3 für die Eingriffsgrenzen die Fehler von Test 1. Wenn K kleiner oder größer als 3 ist, bestehen dargestellte Punkte unter G1' Test 1 nicht, und dargestellte Punkte über G3' bestehen Test 1 nicht.

G1 = INVCDF (0,00135) für eine geometrische Verteilung mit dem Parameter p
G3 = INVCDF (0,99865) für eine geometrische Verteilung mit dem Parameter p; Durchschnitt der dargestellten Punkte
G1' = INVCDF (p1') für eine geometrische Verteilung mit dem Parameter p
G3' = INVCDF (p2') für eine geometrische Verteilung mit dem Parameter p
p1' = CDF (–K) für eine Normalverteilung mit Mittelwert = 0 und Standardabweichung = 1
p2' = CDF (K) für eine Normalverteilung mit Mittelwert = 0 und Standardabweichung = 1

Benneyan-Test

Beim Benneyan-Test wird die Anzahl der aufeinander folgenden dargestellten Punkte gleich der unteren Eingriffsgrenze gezählt; hierbei wird mit der folgenden Formel ein Signal generiert:

Minitab rundet cp auf die nächste ganze Zahl auf und verwendet den resultierenden Wert als Anzahl der aufeinander folgenden Punkte gleich der unteren Eingriffsgrenze, die zum Erzeugen eines Signal benötigt wird.

Siehe Benneyan¹ für weitere Informationen zum Benneyan-Test.

Notation

Begriff	Beschreibung
CDF()	CDF für eine Normalverteilung mit dem Mittelwert 0 und Standardabweichung 1
k	Parameter für Test 1. Der Standardwert ist 3.

¹ J. C. Benneyan (2001). „Performance of Number-Between g-Type Statistical Control Charts for Monitoring Adverse Events“, Health Care Management Science, 4, S. 319−336.