In diesem Thema
Dargestellte Punkte
Korrigierte Anzahlen
Minitab berechnet die korrigierten Anzahlen fehlerhafter Einheiten (ai) wie folgt:
Transformierte Anzahlen
Die korrigierten Anzahlen werden dann gemäß der folgenden Formel transformiert:
Anschließend erstellt Minitab ein Wahrscheinlichkeitsnetz für Standardnormalverteilung der transformierten Anzahlen mit Hilfe der in angegebenen Methode.
Notation
| Begriff | Beschreibung |
|---|---|
| di | Anzahl fehlerhafter Einheiten für Teilgruppe i |
| ni | Größe der Teilgruppe i |
 | durchschnittliche Teilgruppengröße |
Verhältnis zwischen beobachteter Streuung und erwarteter Streuung
Erwartete Streuung
Die erwartete Streuung entspricht der Standardabweichung der transformierten Anzahlen (Xi). Diese ist gleich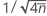 
.
Beobachtete Streuung
Zur Berechnung der beobachteten Streuung berechnet Minitab wie folgt normalverteilte Werte (Y) für die transformierten Anzahlen:
wobei NSCOR die Funktion Normalverteilte Werte ist (verfügbar durch Auswählen von ).
Für den nächsten Schritt werden nur die mittleren 50 % der Xi-Werte zusammen mit deren entsprechenden Yi-Werten verwendet. Xi-Werte werden ausgeschlossen, wenn sie kleiner als das 25. Perzentil oder größer als 75. Perzentil sind.
Minitab passt ein Regressionsmodell kleinster Quadrate mit Yi als Antwortvariable und Xi als Prädiktor an:
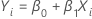
Die beobachtete Streuung beträgt dann 1/β1.
Verhältnis
Das Verhältnis zwischen beobachteter Streuung und erwarteter Streuung wird wie folgt berechnet:
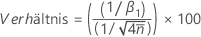
Notation
| Begriff | Beschreibung |
|---|---|
| Xi | transformierte Anzahlen (weitere Informationen finden Sie im Abschnitt „Dargestellte Punkte“) |
 | durchschnittliche Teilgruppengröße |
| β0 | Schnittpunkt mit der y-Achse aus der Gleichung der Regression kleinster Quadrate |
| β1 | Steigungskoeffizient aus der Gleichung der Regression kleinster Quadrate |
95%-Konfidenzgrenzen für Verhältnis
obere Konfidenzgrenze
Die obere Konfidenzgrenze für das Verhältnis wird wie folgt berechnet:
wobei 
der mittlere Anteil fehlerhafter Einheiten ist und wie folgt berechnet wird:
untere Konfidenzgrenze
Für die untere Konfidenzgrenze für das Verhältnis verwendet Minitab einen konservativen festen Wert von 60 %.
Notation
| Begriff | Beschreibung |
|---|---|
| m | Anzahl der Teilgruppen |
 | durchschnittliche Teilgruppengröße |
| di | Anzahl fehlerhafter Einheiten für Teilgruppe i |
| ni | Größe der Teilgruppe i |
Entscheidung
- Wenn Verhältnis > obere Konfidenzgrenze
- Wenn das Verhältnis größer als die obere Konfidenzgrenze ist, kann die Verwendung einer herkömmlichen p-Karte mit den Daten zu einem Anstieg der falschen Alarme führen. In diesem Fall wird eine p'-Karte nach Laney empfohlen.
- Wenn Verhältnis < untere Konfidenzgrenze
- Wenn das Verhältnis kleiner als die untere Konfidenzgrenze ist, kann die Verwendung einer herkömmlichen p-Karte mit den Daten dazu führen, dass die Eingriffsgrenzen zu breit sind. In diesem Fall wird eine p'-Karte nach Laney empfohlen.
