Wählen Sie die gewünschte Methode oder Formel aus.
In diesem Thema
Dargestellte Punkte
Die dargestellten Punkte sind die Fehlerrate für jede Teilgruppe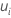 
:
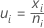
Die Datenpunkte auf einer u-Karte folgen der Poisson-Verteilung.
Notation
| Begriff | Beschreibung |
|---|---|
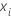 | Anzahl Fehler für Teilgruppe  |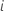
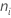 | Größe der Teilgruppe  |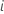
Mittellinie
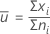
Die Mittellinie ist der Prozessmittelwert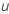 
. Wenn Sie keinen historischen Wert angeben, verwendet Minitab den Mittelwert aus den Daten, 
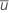, zum Schätzen von 
.
Notation
| Begriff | Beschreibung |
|---|---|
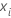 | Anzahl der Fehler in Teilgruppe  |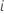
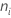 | Größe der Teilgruppe  |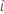
Sigma-Z
Jede Teilgruppenrate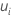 
wird in einen Z-Wert konvertiert (
):
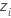Dann wird eine gleitende Spannweite der Länge 2 verwendet, um die Streuung in den Z-Werten auszuwerten und Sigma-Z zu berechnen (
):
Hierbei ist 1,128 eine Konstante für die erwartungstreue Schätzung.
Notation
| Begriff | Beschreibung |
|---|---|
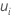 | Fehlerrate für Teilgruppe  |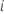
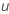 | Prozessmittelwert |
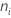 | Größe der Teilgruppe  |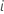
 | gleitende Spannweite der Länge 2 |
Eingriffsgrenzen
Untere Eingriffsgrenze (UEG)
Die UEG für jede Teilgruppe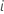 
ist der größere der folgenden Werte:
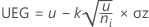
oder
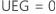
Obere Eingriffsgrenze (OEG)
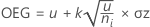
Notation
| Begriff | Beschreibung |
|---|---|
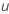 | Prozessmittelwert |
 | Parameter für Test 1. Der Standardwert ist 3. (Weitere Informationen finden Sie unter Auswählen von Tests auf Ausnahmebedingungen für u'-Karte nach Laney.) |
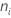 | Größe der Teilgruppe  |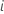
 | siehe „Sigma-Z“ |
