Was ist eine Datentransformation?
Wenn Sie eine auf normalverteilte Daten ausgelegte Prozessfähigkeitsanalyse verwenden, z. B. Prozessfähigkeitsanalyse für Normalverteilung, müssen die Daten einer Normalverteilung folgen. Wenn die Daten nicht normalverteilt sind, sind die Ergebnisse der Analyse nicht genau. In einigen Fällen können Sie nicht normalverteilte Daten transformieren, indem Sie eine Funktion auf die Daten anwenden, die deren Werte so ändert, dass sie einer Normalverteilung besser folgen.
Angenommen, Sie möchten eine Prozessfähigkeitsanalyse für die Auslieferungsdauer von Pizza durchführen. Da die Auslieferung eine Mindestzeit erfordert, es jedoch keine maximale Auslieferungsdauer gibt, sind die Daten rechtsschief. Es kann eine Transformation angewendet werden, um diese starke Schiefe aus den Daten zu entfernen.

Vor der Transformation
Die Auslieferungsdauer weist eine Rechtsschiefe auf und ist anscheinend nicht normalverteilt.
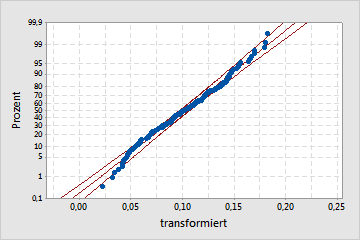
Nach der Transformation
Nachdem die Daten transformiert wurden, folgen sie der Normalverteilung besser.
Was bewirkt die Box-Cox-Transformation?
Die Box-Cox-Transformation ist eine Potenztransformation, W = y**λ, bei der Minitab den besten Wert für λ bestimmt.
Der beste Schätzwert von Lambda (λ) kann zwar eine beliebige Zahl zwischen −5 und 5 sein, in der Praxis empfiehlt sich jedoch ein λ-Wert, der einer verständlichen Transformation entspricht, z. B. die Quadratwurzel (λ=0,5) oder der natürliche Logarithmus (λ=0).
Was bewirkt die Johnson-Transformation?
Bei der Johnson-Transformation wird ein anderer Algorithmus als bei der Box-Cox-Transformation verwendet. Die Johnson-Transformationsfunktion wird aus drei Familien von Funktionen im Johnson-System ausgewählt. Da diese Funktionen durch Änderungen der Parameter eine breite Auswahl von Verteilungen abdecken, findet Minitab in der Regel eine akzeptable Transformation. Die von Minitab ausgewählte Familie wird als bester Transformationstyp bezeichnet.
Durchführen einer Prozessfähigkeitsanalyse für normalverteilte Daten mit einer Datentransformation
Wenn Ihre Daten nicht normalverteilt sind, können Sie versuchen, eine Transformation auszuführen, so dass Sie eine Prozessfähigkeitsanalyse für normalverteilte Daten durchführen können.
- Wählen Sie aus. Klicken Sie auf Transformieren.
- Wählen Sie eine Transformation aus:
- Box-Cox-transformation
- Diese Transformation ist leicht verständlich und bietet Statistiken sowohl für die Prozessfähigkeit innerhalb der Teilgruppen als auch für die Gesamtprozessfähigkeit.
- Johnson-transformation
- Diese Transformation ist äußerst leistungsfähig und kann mit Daten verwendet werden, die Nullwerte und negative Werte enthalten; sie ist jedoch komplizierter und bietet lediglich eine Statistik der Gesamtprozessfähigkeit. Verwenden Sie diese Option, wenn die Box-Cox-Transformation keine geeignete Transformation ermöglicht.
- Geben Sie (optional) Transformationsoptionen an, und klicken Sie anschließend auf OK.
