Z.Bench als Schätzwert der Sigma-Prozessfähigkeit

Sie können Z.Bench-Werte anstelle der Prozessfähigkeitsindizes Cp und Pp verwenden, um die Sigma-Prozessfähigkeit eines Prozesses mit Messdaten zu beschreiben.

In diesem Thema

Was ist Z.Bench?
Welche verschiedenen Z.Bench-Werte gibt es?
So wird Z.Bench abgerufen
Schätzen der Sigma-Prozessfähigkeit mit Hilfe von Z.Bench

Was ist Z.Bench?

Mit Z.Bench-Werten können Sie die Sigma-Prozessfähigkeit eines Prozesses beschreiben. Da sie auf einer Standardnormalverteilung basieren, sind Z.Bench-Statistiken Benchmark-Werte, mit denen Sie die Prozessfähigkeit einfach vergleichen können.

Um ein Verständnis von Z.Bench zu erlangen, betrachten Sie alle Fehler eines Prozesses, die üblicherweise jenseits beider Spezifikationsgrenzen liegen.

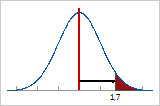
Wenn Sie alle Fehler im rechten Randbereich der Verteilung platzieren und anschließend die Anzahl der Standardabweichungen vom Mittelpunkt bis zu dem Punkt messen, der die Gesamtfehler darstellt, erhalten Sie den Z.Bench-Wert.

Welche verschiedenen Z.Bench-Werte gibt es?

Z.Bench-Statistiken können die Short-Term-Prozessfähigkeit (potenziell) oder die Long-Term-Prozessfähigkeit (Ist) des Prozesses angeben, je nachdem, ob sie mit der Standardabweichung innerhalb oder der Gesamtstandardabweichung berechnet wurden.

Short-Term-Z.Bench (Z.bench_ST): Der Short-Term-Z.Bench wird mit der Standardabweichung innerhalb der Teilgruppen des Prozesses berechnet. Dabei handelt es sich um ein Maß der Leistung des aktuellen Prozesses, wenn die Kurzzeitstreuung konstant gehalten würde (also der Idealfall); dies wird auch als „Process Entitlement“ bezeichnet.
Long-Term-Z.Bench (Z.bench_LT): Der Long-Term-Z.Bench wird mit der Gesamtstandardabweichung des Prozesses berechnet. Dieses Maß bildet die Realität besser ab, da die Kurzzeitstreuung normalerweise nicht über längere Zeiträume konstant gehalten werden kann. Es stellt die Qualität dar, die der Kunde tatsächlich erhält.
Z.Shift: Dies ist die Differenz zwischen Z.Bench_ST und Z.Bench_LT. Je größer der Z.Shift, desto größer sind die Verbesserungsmöglichkeiten, wenn Sie den Prozess besser beherrschen oder die Ausnahmebedingungen für die Streuung zwischen Teilgruppen reduzieren oder beseitigen können.; Statistiker nehmen im Allgemeinen einen Shift von 1,5 σ (Z_ST = Z_LT + 1,5) an.

So wird Z.Bench abgerufen

Wenn Sie über stetige Daten verfügen, können Sie eine Prozessfähigkeitsanalysen bei normalverteilten Daten durchführen und Z.Bench-Statistiken anfordern. Angenommen, die Daten befinden sich in C1, die Teilgruppengröße ist 5, die untere Spezifikationsgrenze ist 598, und die obere Spezifikationsgrenze ist 602. Nehmen Sie außerdem an, dass die Daten aus einer Normalverteilung stammen und der Prozess statistisch beherrscht ist.

Wählen Sie Statistik > Qualitätswerkzeuge > Prozessfähigkeitsanalyse > Normal aus.
Geben Sie im Feld Einzelne Spalte den Wert C1 ein.
Geben Sie im Feld Teilgruppengröße den Wert 5 ein.
Geben Sie im Feld Untere Spezifikationsgrenze den Wert 598 ein. Geben Sie im Feld Obere Spezifikationsgrenze den Wert 602 ein.
Klicken Sie auf Optionen. Wählen Sie Benchmark-Z (σ-Niveau) aus.
Klicken Sie in den einzelnen Dialogfeldern auf OK.

Z.Bench-Statistiken werden in der grafischen Ausgabe unter „Potenzielle Prozessfähigkeit (innerhalb)“ und unter „Gesamtprozessfähigkeit“ angezeigt.

Schätzen der Sigma-Prozessfähigkeit mit Hilfe von Z.Bench

Z.Bench wird häufig verwendet, um die Sigma-Prozessfähigkeit eines Prozesses zu schätzen. Die genaue Methode kann jedoch je nach Branchenpraktiken oder Unternehmensstandards variieren. Einige Fachleute nutzen für die Sigma-Prozessfähigkeit den unter „Potenzielle Prozessfähigkeit (innerhalb)“ angegebenen Short-Term-Z.Bench-Wert, wobei die Standardabweichung innerhalb von Teilgruppen verwendet wird. Andere Fachleute definieren die Sigma-Prozessfähigkeit als 1,5 plus dem unter „Gesamtprozessfähigkeit“ angegebenen Long-Term-Z.Bench-Wert, wobei die Gesamtstandardabweichung des Prozesses verwendet wird. (Wenn beispielsweise der unter „Gesamtprozessfähigkeit“ angegebene Z.Bench-Wert 4 beträgt, ist die Sigma-Prozessfähigkeit 4 + 1,5 = 5,5.) Informieren Sie sich daher in Bezug auf die Sigma-Prozessfähigkeit über die konkreten Richtlinien im Unternehmen bzw. der Branche.

Mit Hilfe der Z.Bench-Werte können Sie andere Prozessfähigkeitsmaße für Ihren Prozess bestimmen. In dieser Tabelle wird die Beziehung zwischen Z.Bench-Werten und anderen Maßen für die Prozessfähigkeit gezeigt.

Z.Bench	Sigma-Prozessfähigkeit	PPM fehlerhafte Einheiten
1	2,5 σ	158.655
2	3,5 σ	22.750
3	4,5 σ	1.350
4	5,5 σ	32
4,5	6,0 σ	3,4

Hinweis

In der Tabelle wird die Sigma-Prozessfähigkeit unter Annahme eines Z-Shift von 1,5 σ berechnet.