In diesem Thema
Pp

Notation
| Begriff | Beschreibung |
|---|---|
| OSG | Obere Spezifikationsgrenze |
| USG | Untere Spezifikationsgrenze |
| Toler | Multiplikator der Sigma-Toleranz (Standardwert in Minitab ist 6) |
 | Gesamtstandardabweichung |
Ppk

Cpm
Cpm ist nur verfügbar, wenn ein Sollwert angegeben wurde. Minitab berechnet den Cpm-Wert auf der Grundlage bekannter Werte für USG, OSG und T.
| Bekannter Wert | Cpm |
|---|---|
| Nur USG und OSG | * |
| USG, OSG und T = m |
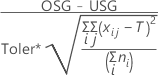 |
| USG, OSG und T ≠ m |
 |
| Nur OSG und T |
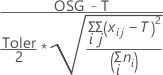 |
| Nur USG und T |
 |
| Nur USG oder OSG | * |
Notation
| Begriff | Beschreibung |
|---|---|
| * | Fehlender Wert |
| OSG | Obere Spezifikationsgrenze |
| USG | Untere Spezifikationsgrenze |
| m | Mittelpunkt zwischen OSG und USG |
| T | Sollwert |
| Xij | j-te Beobachtung in der i-ten Teilgruppe |
| ni | Anzahl der Beobachtungen in der i-ten Teilgruppe |
| Toler | Multiplikator der Sigma-Toleranz (Standardwert in Minitab ist 6) |
PPM gesamt für erwartete Leistung (gesamt)
Die auf der Grundlage der Gesamtstreuung des Prozesses erwartete Anzahl der Teile pro Million, die außerhalb der Spezifikationsgrenzen liegen, beträgt:


Notation
| Begriff | Beschreibung |
|---|---|
| PPM | Teile pro Million |
| USG | Untere Spezifikationsgrenze |
| OSG | Obere Spezifikationsgrenze |
| Φ (X) | Kumulative Verteilungsfunktion (CDF) einer Standardnormalverteilung |
 | Durchschnitt der Beobachtungen |
| s | Gesamtstandardabweichung |
Z.USG, Z.OSG und Z.Bench für die Gesamtprozessfähigkeit
Benchmark-Z-Statistiken für die Gesamtprozessfähigkeit werden berechnet, indem der Z-Wert auf der Grundlage der Standardnormalverteilung (0;1) für die entsprechenden Statistiken ermittelt wird.



Dabei gilt Folgendes:


Notation
| Begriff | Beschreibung |
|---|---|
| Φ (X) | Kumulative Verteilungsfunktion (CDF) einer Standardnormalverteilung |
| Φ-1 (X) | Inverse CDF einer Standardnormalverteilung |
 | Gesamtstandardabweichung |
