Pp
Pp wird anhand der angegebenen Parameterwerte berechnet oder mit der Maximum Likelihood-Methode für eine in der Analyse verwendete Verteilung geschätzt. Minitab berechnet die Pp-Statistik entweder mit der z-Werte-Methode (Standardeinstellung) oder mit der ISO-Methode, je nachdem, welche Einstellungen in ausgewählt wurden. Die folgenden Formeln basieren auf der Standardtoleranz von K = 6, die 6 Standardabweichungen breit ist (3 Standardabweichungen auf jeder Seite des Prozessmittelwerts).
z-Werte-Methode

Notation
| Begriff | Beschreibung |
|---|---|
| Z.USG | Φ–1(p1) |
| Z.OSG | Φ–1(p2) |
| Φ–1(p) | p * 100-tes Perzentil einer Standardnormalverteilung |
| p1 | Wahrsch (X ≤ USG) |
| p2 | Wahrsch (X ≤ OSG) |
| X | X folgt der in der Analyse verwendeten Verteilung |
ISO-Methode
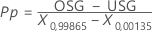
Notation
| Begriff | Beschreibung |
|---|---|
| OSG | Obere Spezifikationsgrenze |
| USG | Untere Spezifikationsgrenze |
| X0,99865 | 99,865-tes Perzentil für die angegebene Verteilung |
| X0,00135 | 0,135-tes Perzentil für die angegebene Verteilung |
Ppk

PPM gesamt für erwartete Leistung (gesamt)
Die erwartete Anzahl der Teile pro Million, die außerhalb der Spezifikationsgrenzen liegen, wird wie folgt berechnet:
PPM gesamt (erw. Gesamtleistung) = PPM < USG (erw. Gesamtleistung) + PPM > OSG (erw. Gesamtleistung)
PPM gesamt (erw. Gesamtleistung) = [1.000.000 * F(USG)]+ [1.000.000 * (1 – F(OSG))]
Notation
| Begriff | Beschreibung |
|---|---|
| F(X) | Die kumulative Verteilungsfunktion (CDF) der in der Analyse verwendeten Verteilung, basierend auf geschätzten oder angegebenen Parametern |
| USG | Untere Spezifikationsgrenze |
| OSG | Obere Spezifikationsgrenze |
| PPM | Teile pro Million |
Z.Bench, Z.USG, Z.OSG
Benchmark-Z-Statistiken für die Gesamtprozessfähigkeit werden berechnet, indem der Z-Wert auf der Grundlage der Standardnormalverteilung (0;1) für die entsprechenden Statistiken ermittelt wird.


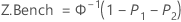
Hinweis
PPL und PPU basieren auf der für die Analyse verwendeten Methode (ISO oder Minitab). Weitere Informationen finden Sie unter Methoden und Formeln für Maße der Gesamtprozessfähigkeit in Prozessfähigkeitsanalyse (nicht normal). Die Formeln basieren auf der Standardtoleranz von K = 6, die 6 Standardabweichungen breit ist (3 Standardabweichungen auf jeder Seite des Prozessmittelwerts).
Notation
| Begriff | Beschreibung |
|---|---|
| P1 | Wahrscheinlichkeit (Beobachtungen < USG) basierend auf der in der Analyse verwendeten Nicht-Normalverteilung und den von Ihnen angegebenen Parametern (oder den aus den Daten geschätzten Parametern) |
| P2 | Wahrscheinlichkeit (Beobachtungen > OSG) basierend auf der in der Analyse verwendeten Nicht-Normalverteilung und den von Ihnen angegebenen Parametern (oder den aus den Daten geschätzten Parametern) |
| Φ (X) | Kumulative Verteilungsfunktion (CDF) einer Standardnormalverteilung |
| Φ–1 (X) | Inverse CDF einer Standardnormalverteilung |
