In diesem Thema
Schritt 1: Bestimmen, ob der Prozess stabil ist
Der Prozess muss stabil sein, damit Sie zuverlässige Schätzwerte der Prozessfähigkeit erhalten.
Mit Regelkarten können Sie die Stabilität Ihres Prozesses überwachen, indem Sie Punkte außer Kontrolle sowie Muster und Trends in den Daten identifizieren.
Rote Punkte zeigen Teilgruppen an, die mindestens einen Test auf Ausnahmebedingungen nicht bestehen und außer Kontrolle sind. Punkte außer Kontrolle weisen darauf hin, dass der Prozess möglicherweise nicht stabil ist und die Ergebnisse der Prozessfähigkeitsanalyse u. U. nicht zuverlässig sind. Sie sollten die Ursache für die Punkte außer Kontrolle ermitteln und Streuungen durch Ausnahmebedingungen entfernen, bevor Sie die Prozessfähigkeit analysieren.
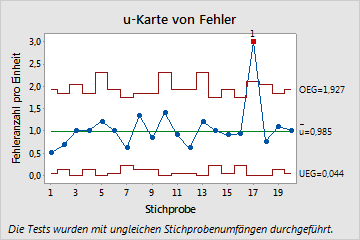
Auf dieser u-Karte sind die meisten Punkte zufällig gestreut und liegen innerhalb der Eingriffsgrenzen. Es lassen sich weder Trends noch Muster erkennen. Die Fehlerrate pro Einheit für Tag 17 ist jedoch nicht unter Kontrolle. Bevor Sie die Prozessfähigkeit des Prozesses bewerten, untersuchen und beseitigen Sie sämtliche Ausnahmebedingungen, die an dem betreffenden Tag zu der außergewöhnlich hohen DPU beigetragen haben können.
Schritt 2: Ermitteln, ob die Daten einer Poisson-Verteilung folgen
Bevor Sie die Prozessfähigkeit des Prozesses auswerten, ermitteln Sie, ob dieser einer Poisson-Verteilung folgt. Wenn die Daten keiner Poisson-Verteilung folgen, sind die Schätzwerte der Prozessfähigkeit möglicherweise nicht zuverlässig. Es hängt davon ab, ob die Teilgruppengrößen gleich oder unterschiedlich sind, welche Grafik Minitab zum Beurteilen der Verteilung der Daten anzeigt.
Teilgruppengrößen sind gleich
Wenn alle Teilgruppengrößen gleich sind, zeigt Minitab ein Poisson-Diagramm an.
Untersuchen Sie das Diagramm, um festzustellen, ob die dargestellten Punkte annähernd einer Geraden folgen. Wenn dies nicht der Fall ist, ist die Annahme, dass die Stichprobe der Daten aus einer Poisson-Verteilung stammt, möglicherweise falsch.
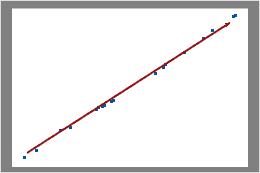
Poisson
In diesem Diagramm sind die Datenpunkte eng an der Linie ausgerichtet. Sie können annehmen, dass die Daten einer Poisson-Verteilung folgen.
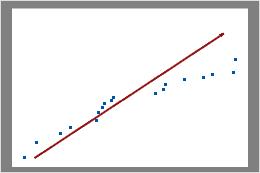
Nicht Poisson
In diesem Diagramm sind die Datenpunkte nicht eng an der Linie in der oberen rechten Ecke des Diagramms ausgerichtet. Diese Daten folgen keiner Poisson-Verteilung, und sie können mit einer Prozessfähigkeitsanalyse (Poisson) nicht zuverlässig ausgewertet werden.
Teilgruppengrößen sind ungleich
Bei unterschiedlichen Teilgruppengrößen zeigt Minitab ein Diagramm der Fehlerrate an.
Untersuchen Sie das Diagramm, um auszuwerten, ob die Fehler pro Einheit (DPU) zufällig über alle Stichprobenumfänge gestreut sind oder ob ein Muster vorliegt. Wenn die Daten zufällig um die Mittellinie verteilt sind, können Sie daraus schließen, dass sie einer Poisson-Verteilung folgen.
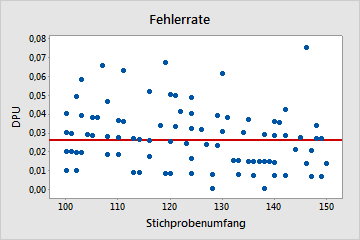
Poisson
In diesem Diagramm sind die Punkte zufällig um die Mittellinie gestreut. Sie können annehmen, dass die Daten einer Poisson-Verteilung folgen. Daher können die Daten mit einer Prozessfähigkeitsanalyse (Poisson) untersucht werden.
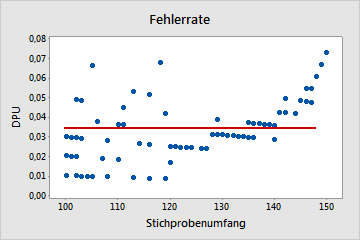
Nicht Poisson
In diesem Diagramm ist das Muster nicht zufällig. Bei größeren Stichprobenumfängen als 120 nimmt der DPU bei zunehmendem Stichprobenumfang ebenfalls zu. Dieses Ergebnis verweist auf eine mögliche Korrelation zwischen Stichprobenumfang und Fehlerrate. Daher folgen die Daten keiner Poisson-Verteilung, und sie können mit einer Prozessfähigkeitsanalyse (Poisson) nicht zuverlässig ausgewertet werden.
Schritt 3: Mittlere Fehler pro Einheit (DPU) auswerten
Untersuchen des Schätzwerts von Mittlerer DPU und des KI
Mit dem mittleren DPU der Stichprobendaten können Sie den mittleren DPU des Prozesses schätzen. Verwenden Sie das Konfidenzintervall als Fehlerspanne für den Schätzwert.
Das Konfidenzintervall liefert einen Bereich wahrscheinlicher Werte für den tatsächlichen Wert des mittleren DPU im Prozess (wenn alle produzierten Einheiten erfasst und analysiert werden könnten). Bei einem 95%-Konfidenzniveau können Sie sich zu 95 % sicher sein, dass der tatsächliche mittlere DPU des Prozesses innerhalb des Konfidenzintervalls liegt. Das heißt, wenn Sie 100 Zufallsstichproben aus dem Prozess erfassen, können Sie erwarten, dass etwa 95 der Stichproben Intervalle liefern, die den tatsächlichen Wert des mittleren DPU enthalten.
Anhand des Konfidenzintervalls können Sie die praktische Signifikanz Ihres Stichprobenschätzwerts beurteilen. Wenn ein maximal zulässiger Wert für den mittleren DPU vorliegt, dem Ihre Prozesskenntnis oder Branchenstandards zugrunde liegen, vergleichen Sie die obere Konfidenzgrenze mit diesem Wert. Wenn die obere Konfidenzgrenze unter dem maximal zulässigen Wert für den mittleren DPU liegt, können Sie sicher sein, dass der Prozess die Spezifikationen erfüllt, selbst wenn der Einfluss der Streuung aufgrund der Zufälligkeit der Stichproben auf den Schätzwert berücksichtigt wird.
Wichtigste Ergebnisse: Mittlerer DPU, KI
Die Ergebnisse für die Prozessfähigkeitsanalyse (Poisson) umfassen die Tabelle „Zusammenfassende Statistik“, die sich im unteren mittleren Teil der Ausgabe befindet. In dieser simulierten Tabelle „Zusammenfassende Statistik“ gibt der Soll-DPU (0,0250) den maximal zulässigen DPU für den Prozess an. Der geschätzte mittlere DPU beträgt 0,0225 und liegt somit unter dem maximal zulässigen Wert. Die Obergrenze KI für den mittleren DPU beträgt jedoch 0,0265 und überschreitet damit den maximal zulässigen Wert. Daher können Sie nicht mit einer Sicherheit von 95 % behaupten, dass der Prozess fähig ist. Sie müssen u. U. einen größeren Stichprobenumfang verwenden oder die Streuung des Prozesses verringern, um ein schmaleres Konfidenzintervall für den Schätzwert des mittleren DPU zu erhalten.
| Zusammenfassende Statistik | |
|---|---|
| (95,0 % Konfidenz) | |
| Mittlerer DPU: | 0,0225 |
| Untergrenze KI: | 0,0190 |
| Obergrenze KI: | 0,0265 |
| Min.-DPU: | 0,0000 |
| Max.-DPU: | 0,0661 |
| Soll-DPU: | 0,0250 |
Bestimmen, ob eine ausreichende Menge von Daten für einen zuverlässigen Schätzwert vorhanden ist
Mit dem Diagramm des kumulierten DPU können Sie feststellen, ob Sie eine ausreichende Anzahl von Stichproben erfasst haben, um einen stabilen Schätzwert des DPU zu erhalten.
Untersuchen Sie die Fehler pro Einheit für die chronologisch angeordneten Stichproben, um festzustellen, wie sich der Schätzwert bei Erfassung weiterer Stichproben ändert. Im Idealfall stabilisiert sich der DPU nach einigen Stichproben; dies wird durch das Abflachen der dargestellten Punkte entlang der Linie des mittleren DPU veranschaulicht.
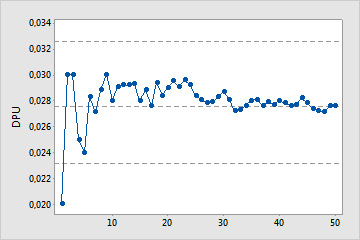
Ausreichende Anzahl von Stichproben
In diesem Diagramm stabilisiert sich der DPU entlang der Linie für den mittleren DPU. Daher enthält die Prozessfähigkeitsanalyse genügend Stichproben, um einen stabilen, zuverlässigen Schätzwert des mittleren DPU zu erhalten.
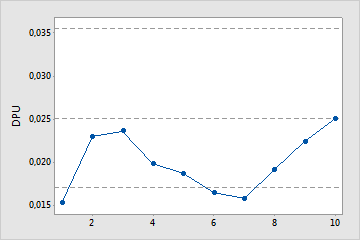
Keine ausreichende Anzahl von Stichproben
In diesem Diagramm stabilisiert sich der DPU nicht. Daher enthält die Prozessfähigkeitsanalyse keine ausreichende Anzahl von Stichproben, um den mittleren DPU zuverlässig zu schätzen.
