In diesem Thema
Schätzen der Standardabweichung
Bei der Prozessfähigkeitsanalyse (Normalverteilung) werden die Standardabweichung innerhalb von Teilgruppen und die Gesamtstandardabweichung geschätzt.
Standardabweichung innerhalb von Teilgruppen
Die Methode zum Schätzen von σinnerhalb hängt von der Teilgruppengröße ab.
- Zusammengefasste Standardabweichung:

Dabei gilt Folgendes:


Hinweis
Wenn Sie die Standardmethode ändern und sich dafür entscheiden, die Konstante für die erwartungstreue Schätzung nicht zu verwenden, wird σinnerhalb anhand von Sp geschätzt.
Begriff Beschreibung d Freiheitsgrade für Sp= Σ (ni– 1) Xij j-te Beobachtung in der i-ten Teilgruppe X̅i Mittelwert der i-ten Teilgruppe ni Anzahl der Beobachtungen in der i-ten Teilgruppe C4(d+1) Konstante für erwartungstreue Schätzung Γ(·) Gamma-Funktion - Durchschnitt der Teilgruppenspannweiten (R-quer):

Dabei gilt Folgendes:


Bei Gleichheit aller n:
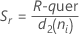
Begriff Beschreibung ri Spannweite der i-ten Teilgruppe d2 (ni) Eine aus einer Tabelle ausgelesene Konstante für die erwartungstreue Schätzung (weitere Informationen finden Sie im Abschnitt zu den Konstanten für die erwartungstreue Schätzung d2(), d3() und d4()) d3 (ni) Eine aus einer Tabelle ausgelesene Konstante für die erwartungstreue Schätzung (weitere Informationen finden Sie im Abschnitt zu den Konstanten für die erwartungstreue Schätzung d2(), d3() und d4()) ni Anzahl der Beobachtungen in der i-ten Teilgruppe - Durchschnitt der Teilgruppenstandardabweichungen (S-quer):

Dabei gilt Folgendes:
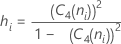
Hinweis
Wenn Sie die Standardeinstellung ändern und die Konstante für die erwartungstreue Schätzung nicht verwenden, wird σinnerhalb anhand von Σ Si / Anzahl der Teilgruppen geschätzt.
Begriff Beschreibung C4(ni) Konstante für erwartungstreue Schätzung (gemäß Definition für die zusammengefasste Standardabweichung) Si Standardabweichung von Teilgruppe i ni Anzahl der Beobachtungen in der i-ten Teilgruppe
- Mittelwert der gleitenden Spannweite:
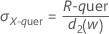
Dabei gilt Folgendes:

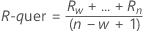
Begriff Beschreibung Ri i-te gleitende Spannweite w Anzahl der Beobachtungen in der gleitenden Spannweite. Die Standardeinstellung lautet w = 2. d2(w) Eine aus einer Tabelle ausgelesene Konstante für die erwartungstreue Schätzung (weitere Informationen finden Sie im Abschnitt zu den Konstanten für die erwartungstreue Schätzung d2(), d3() und d4()) - Median der gleitenden Spannweite:

Dabei gilt Folgendes:

Begriff Beschreibung MRi i-te gleitende Spannweite MR-quer̅ Median von MRi w Anzahl der Beobachtungen in der gleitenden Spannweite. Die Standardeinstellung lautet w = 2. d4(w) Eine aus einer Tabelle ausgelesene Konstante für die erwartungstreue Schätzung (weitere Informationen finden Sie im Abschnitt zu den Konstanten für die erwartungstreue Schätzung d2(), d3() und d4()) - Quadratwurzel des Mittels der quadrierten sukzessiven Differenzen (MSSD):

Hinweis
Wenn Sie die Standardeinstellung ändern und die Konstante für die erwartungstreue Schätzung nicht verwenden, wird σinnerhalb wie folgt geschätzt:

Begriff Beschreibung di Sukzessive Differenzen C4(ni) Konstante für erwartungstreue Schätzung (gemäß Definition für die zusammengefasste Standardabweichung) C4'(ni) Konstante für die erwartungstreue Schätzung ≈ c4(ni) (weitere Informationen finden Sie im Abschnitt zur Konstanten für die erwartungstreue Schätzung c4'()) N Gesamtzahl der Beobachtungen ni Anzahl der Beobachtungen in der i-ten Teilgruppe
Gesamtstandardabweichung

Dabei gilt Folgendes:
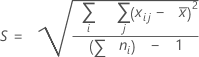
Hinweis
Standardmäßig verwendet Minitab die Konstante für die erwartungstreue Schätzung beim Schätzen von σgesamt nicht. σgesamt wird anhand von S geschätzt. Wenn Sie die Gesamtstandardabweichung mit der Konstanten für die erwartungstreue Schätzung schätzen möchten, können Sie diese Option beim Durchführen der Prozessfähigkeitsanalyse im Unterdialogfeld Schätzen ändern. Wenn Minitab die Konstante für die erwartungstreue Schätzung generell standardmäßig verwenden soll, wählen Sie und anschließend die entsprechenden Optionen aus.
| Begriff | Beschreibung |
|---|---|
| xij | j-te Beobachtung in der i-ten Teilgruppe |
| x̅ | Prozessmittelwert |
| ni | Anzahl der Beobachtungen in der i-ten Teilgruppe |
| C4 (N) | Konstante für erwartungstreue Schätzung (gemäß Definition für die zusammengefasste Standardabweichung) |
| N (oder Σ ni) | Gesamtzahl der Beobachtungen |
Box-Cox-Transformation
Mit der Box-Cox-Transformation wird ein Lambda-Wert geschätzt (wie in der folgenden Tabelle veranschaulicht), der die Standardabweichung einer standardisierten transformierten Variablen minimiert. Die resultierende Transformation ist Yλ, wenn λ ҂ 0; sie ist ln Y, wenn λ = 0.
Bei der Box-Cox-Methode werden viele Arten von Transformationen durchsucht. In der folgenden Tabelle sind einige der gängigsten Transformationen aufgeführt, wobei Y' die Transformation des Y der Daten darstellt.
| Lambda-Wert (λ) | Transformation |
|---|---|
 |
 |
 |
 |
 |
 |
 |
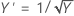 |
 |
 |
Algorithmus für die Johnson-Transformation
Bei der Johnson-Transformation wird die optimale Verteilung aus drei Familien von Verteilungen ausgewählt, um die Daten so zu transformieren, dass sie einer Normalverteilung folgen.
| Johnson-Familie | Transformationsfunktion | Spannweite |
|---|---|---|
| SB | γ + η ln [(x – ε) / (λ + ε – x)] | η, λ > 0, –∞ < γ < ∞ , –∞ < ε < ∞, ε < x < ε + λ |
| SL | γ + η ln (x – ε) | η > 0, –∞ < γ < ∞, –∞ < ε < ∞, ε < x |
| SU | γ + η Sinh–1 [(x – ε) / λ] , wobei
Sinh–1(x) = ln [x + sqrt (1 + x2)] |
η, λ > 0, –∞ < γ < ∞, –∞ < ε < ∞, –∞ < x < ∞ |
Der Algorithmus verwendet folgendes Verfahren:
- Es werden nahezu alle potenziellen Transformationsfunktionen des Johnson-Systems berücksichtigt.
- Die Parameter in der Funktion werden anhand der in Chou et al.1 beschriebenen Methode geschätzt.
- Die Daten werden unter Verwendung der Transformationsfunktion transformiert.
- Für die transformierten Daten werden die Anderson-Darling-Statistik und der entsprechende p-Wert berechnet.
- Es wird die Transformationsfunktion mit dem größten p-Wert ausgewählt, der größer als der im Dialogfeld Transformieren angegebene p-Wert ist (Standardwert 0,10). Andernfalls ist keine Transformation angemessen.
Notation
| Begriff | Beschreibung |
|---|---|
| SB | Verteilung der Johnson-Familie mit begrenzter Variable (B) |
| SL | Verteilung der Johnson-Familie mit lognormaler Variable (L) |
| SU | Verteilung der Johnson-Familie mit unbegrenzter Variable (B) |
Weitere Informationen zur Johnson-Transformation finden Sie in Chou et al.1 In Minitab wurde der Shapiro-Wilks-Test auf Normalverteilung durch den Anderson-Darling-Test ersetzt.
Weitere Informationen zum Wahrscheinlichkeitsnetz, zu den Perzentilen und deren Konfidenzintervallen finden Sie unter Methoden und Formeln für Verteilungen in Identifikation der Verteilung.
Konstanten für erwartungstreue Schätzung d2(), d3() und d4()
d2(N) ist der erwartete Wert der Spannweite von N Beobachtungen aus einer normalverteilten Grundgesamtheit mit Standardabweichung = 1. Wenn also r die Spannweite einer Stichprobe von N Beobachtungen aus einer Normalverteilung mit Standardabweichung = σ ist, dann ist E(r) = d2(N)σ.
d3(N) ist die Standardabweichung der Spannweite von N Beobachtungen aus einer normalverteilten Grundgesamtheit mit σ = 1. Wenn also r die Spannweite einer Stichprobe von N Beobachtungen aus einer Normalverteilung mit Standardabweichung = σ ist, dann ist StdAbw(r) = d3(N)σ.
Suchen Sie in der folgenden Tabelle eine Konstante für die erwartungstreue Schätzung für einen bestimmten Wert N. (Ziehen Sie zum Bestimmen des Werts von N die Formel für die betreffende Statistik hinzu.)

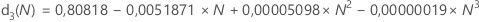

- D. J. Wheeler und D. S. Chambers. (1992). Understanding Statistical Process Control, Second Edition, SPC Press, Inc.
- H. Leon Harter (1960). „Tables of Range and Studentized Range“. The Annals of Mathematical Statistics, Vol. 31, Nr. 4, Institute of Mathematical Statistics, S. 1122−1147.
| N | d2(N) | d3(N) | d4(N) |
|---|---|---|---|
| 2 | 1,128 | 0,8525 | 0,954 |
| 3 | 1,693 | 0,8884 | 1,588 |
| 4 | 2,059 | 0,8798 | 1,978 |
| 5 | 2,326 | 0,8641 | 2,257 |
| 6 | 2,534 | 0,848 | 2,472 |
| 7 | 2,704 | 0,8332 | 2,645 |
| 8 | 2,847 | 0,8198 | 2,791 |
| 9 | 2,970 | 0,8078 | 2,915 |
| 10 | 3,078 | 0,7971 | 3,024 |
| 11 | 3,173 | 0,7873 | 3,121 |
| 12 | 3,258 | 0,7785 | 3,207 |
| 13 | 3,336 | 0,7704 | 3,285 |
| 14 | 3,407 | 0,7630 | 3,356 |
| 15 | 3,472 | 0,7562 | 3,422 |
| 16 | 3,532 | 0,7499 | 3,482 |
| 17 | 3,588 | 0,7441 | 3,538 |
| 18 | 3,640 | 0,7386 | 3,591 |
| 19 | 3,689 | 0,7335 | 3,640 |
| 20 | 3,735 | 0,7287 | 3,686 |
| 21 | 3,778 | 0,7242 | 3,730 |
| 22 | 3,819 | 0,7199 | 3,771 |
| 23 | 3,858 | 0,7159 | 3,811 |
| 24 | 3,895 | 0,7121 | 3,847 |
| 25 | 3,931 | 0,7084 | 3,883 |
| N | d2(N) |
|---|---|
| 26 | 3,964 |
| 27 | 3,997 |
| 28 | 4,027 |
| 29 | 4,057 |
| 30 | 4,086 |
| 31 | 4,113 |
| 32 | 4,139 |
| 33 | 4,165 |
| 34 | 4,189 |
| 35 | 4,213 |
| 36 | 4,236 |
| 37 | 4,259 |
| 38 | 4,280 |
| 39 | 4,301 |
| 40 | 4,322 |
| 41 | 4,341 |
| 42 | 4,361 |
| 43 | 4,379 |
| 44 | 4,398 |
| 45 | 4,415 |
| 46 | 4,433 |
| 47 | 4,450 |
| 48 | 4,466 |
| 49 | 4,482 |
| 50 | 4,498 |
Konstanten für erwartungstreue Schätzung c4() und c5()
c4()

c5()

Notation
| Begriff | Beschreibung |
|---|---|
| Γ() | Gamma-Funktion |
Konstante für erwartungstreue Schätzung c4'()
Entnehmen Sie den folgenden Tabellen Werte für die Konstante für die erwartungstreue Schätzung c4'(), die in den Formeln für die Schätzmethode für Sigma auf der Grundlage der Quadratwurzel von MSSD verwendet wird.
| N | c4'(N) | N | c4'(N) | N | c4'(N) |
|---|---|---|---|---|---|
| 2 | 0,797850 | 41 | 0,990797 | 80 | 0,995215 |
| 3 | 0,871530 | 42 | 0,991013 | 81 | 0,995272 |
| 4 | 0,905763 | 43 | 0,991218 | 82 | 0,995328 |
| 5 | 0,925222 | 44 | 0,991415 | 83 | 0,995383 |
| 6 | 0,937892 | 45 | 0,991602 | 84 | 0,995436 |
| 7 | 0,946837 | 46 | 0,991782 | 85 | 0,995489 |
| 8 | 0,953503 | 47 | 0,991953 | 86 | 0,995539 |
| 9 | 0,958669 | 48 | 0,992118 | 87 | 0,995589 |
| 10 | 0,962793 | 49 | 0,992276 | 88 | 0,995638 |
| 11 | 0,966163 | 50 | 0,992427 | 89 | 0,995685 |
| 12 | 0,968968 | 51 | 0,992573 | 90 | 0,995732 |
| 13 | 0,971341 | 52 | 0,992713 | 91 | 0,995777 |
| 14 | 0,973375 | 53 | 0,992848 | 92 | 0,995822 |
| 15 | 0,975137 | 54 | 0,992978 | 93 | 0,995865 |
| 16 | 0,976679 | 55 | 0,993103 | 94 | 0,995908 |
| 17 | 0,978039 | 56 | 0,993224 | 95 | 0,995949 |
| 18 | 0,979249 | 57 | 0,993340 | 96 | 0,995990 |
| 19 | 0,980331 | 58 | 0,993452 | 97 | 0,996030 |
| 20 | 0,981305 | 59 | 0,993561 | 98 | 0,996069 |
| 21 | 0,982187 | 60 | 0,993666 | 99 | 0,996108 |
| 22 | 0,982988 | 61 | 0,993767 | 100 | 0,996145 |
| 23 | 0,983720 | 62 | 0,993866 | 101 | 0,996182 |
| 24 | 0,984391 | 63 | 0,993961 | 102 | 0,996218 |
| 25 | 0,985009 | 64 | 0,994053 | 103 | 0,996253 |
| 26 | 0,985579 | 65 | 0,994142 | 104 | 0,996288 |
| 27 | 0,986107 | 66 | 0,994229 | 105 | 0,996322 |
| 28 | 0,986597 | 67 | 0,994313 | 106 | 0,996356 |
| 29 | 0,987054 | 68 | 0,994395 | 107 | 0,996389 |
| 30 | 0,987480 | 69 | 0,994474 | 108 | 0,996421 |
| 31 | 0,987878 | 70 | 0,994551 | 109 | 0,996452 |
| 32 | 0,988252 | 71 | 0,994626 | 110 | 0,996483 |
| 33 | 0,988603 | 72 | 0,994699 | 111 | 0,996514 |
| 34 | 0,988934 | 73 | 0,994769 | 112 | 0,996544 |
| 35 | 0,989246 | 74 | 0,994838 | 113 | 0,996573 |
| 36 | 0,989540 | 75 | 0,994905 | 114 | 0,996602 |
| 37 | 0,989819 | 76 | 0,994970 | 115 | 0,996631 |
| 38 | 0,990083 | 77 | 0,995034 | 116 | 0,996658 |
| 39 | 0,990333 | 78 | 0,995096 | 117 | 0,996686 |
| 40 | 0,990571 | 79 | 0,995156 | 118 | 0,996713 |
| N | c4'(N) | N | c4'(N) | N | c4'(N) |
|---|---|---|---|---|---|
| 119 | 0,996739 | 160 | 0,997541 | 201 | 0,998016 |
| 120 | 0,996765 | 161 | 0,997555 | 202 | 0,998025 |
| 121 | 0,996791 | 162 | 0,997570 | 203 | 0,998034 |
| 122 | 0,996816 | 163 | 0,997584 | 204 | 0,998043 |
| 123 | 0,996841 | 164 | 0,997598 | 205 | 0,998052 |
| 124 | 0,996865 | 165 | 0,997612 | 206 | 0,998061 |
| 125 | 0,996889 | 166 | 0,997625 | 207 | 0,998070 |
| 126 | 0,996913 | 167 | 0,997639 | 208 | 0,998078 |
| 127 | 0,996936 | 168 | 0,997652 | 209 | 0,998087 |
| 128 | 0,996959 | 169 | 0,997665 | 210 | 0,998095 |
| 129 | 0,996982 | 170 | 0,997678 | 211 | 0,998104 |
| 130 | 0,997004 | 171 | 0,997691 | 212 | 0,998112 |
| 131 | 0,997026 | 172 | 0,997703 | 213 | 0,998120 |
| 132 | 0,997047 | 173 | 0,997716 | 214 | 0,998128 |
| 133 | 0,997069 | 174 | 0,997728 | 215 | 0,998137 |
| 134 | 0,997089 | 175 | 0,997741 | 216 | 0,998145 |
| 135 | 0,997110 | 176 | 0,997753 | 217 | 0,998152 |
| 136 | 0,997130 | 177 | 0,997765 | 218 | 0,998160 |
| 137 | 0,997150 | 178 | 0,997776 | 219 | 0,998168 |
| 138 | 0,997170 | 179 | 0,997788 | 220 | 0,998176 |
| 139 | 0,997189 | 180 | 0,997800 | 221 | 0,998184 |
| 140 | 0,997209 | 181 | 0,997811 | 222 | 0,998191 |
| 141 | 0,997227 | 182 | 0,997822 | 223 | 0,998199 |
| 142 | 0,997246 | 183 | 0,997834 | 224 | 0,998206 |
| 143 | 0,997264 | 184 | 0,997845 | 225 | 0,998214 |
| 144 | 0,997282 | 185 | 0,997856 | 226 | 0,998221 |
| 145 | 0,997300 | 186 | 0,997866 | 227 | 0,998228 |
| 146 | 0,997318 | 187 | 0,997877 | 228 | 0,998235 |
| 147 | 0,997335 | 188 | 0,997888 | 229 | 0,998242 |
| 148 | 0,997352 | 189 | 0,997898 | 230 | 0,998250 |
| 149 | 0,997369 | 190 | 0,997909 | 231 | 0,998257 |
| 150 | 0,997386 | 191 | 0,997919 | 232 | 0,998263 |
| 151 | 0,997402 | 192 | 0,997929 | 233 | 0,998270 |
| 152 | 0,997419 | 193 | 0,997939 | 234 | 0,998277 |
| 153 | 0,997435 | 194 | 0,997949 | 235 | 0,998284 |
| 154 | 0,997450 | 195 | 0,997959 | 236 | 0,998291 |
| 155 | 0,997466 | 196 | 0,997969 | 237 | 0,998297 |
| 156 | 0,997481 | 197 | 0,997978 | 238 | 0,998304 |
| 157 | 0,997497 | 198 | 0,997988 | 239 | 0,998311 |
| 158 | 0,997512 | 199 | 0,997997 | 240 | 0,998317 |
| 159 | 0,997526 | 200 | 0,998007 | 241 | 0,998323 |
| N | c4'(N) | N | c4'(N) | N | c4'(N) |
|---|---|---|---|---|---|
| 242 | 0,998330 | 283 | 0,998553 | 324 | 0,998720 |
| 243 | 0,998336 | 284 | 0,998558 | 325 | 0,998723 |
| 244 | 0,998342 | 285 | 0,998562 | 326 | 0,998727 |
| 245 | 0,998349 | 286 | 0,998567 | 327 | 0,998730 |
| 246 | 0,998355 | 287 | 0,998571 | 328 | 0,998734 |
| 247 | 0,998361 | 288 | 0,998576 | 329 | 0,998737 |
| 248 | 0,998367 | 289 | 0,998580 | 330 | 0,998740 |
| 249 | 0,998373 | 290 | 0,998585 | 331 | 0,998744 |
| 250 | 0,998379 | 291 | 0,998589 | 332 | 0,998747 |
| 251 | 0,998385 | 292 | 0,998593 | 333 | 0,998751 |
| 252 | 0,998391 | 293 | 0,998598 | 334 | 0,998754 |
| 253 | 0,998397 | 294 | 0,998602 | 335 | 0,998757 |
| 254 | 0,998403 | 295 | 0,998606 | 336 | 0,998761 |
| 255 | 0,998408 | 296 | 0,998611 | 337 | 0,998764 |
| 256 | 0,998414 | 297 | 0,998615 | 338 | 0,998767 |
| 257 | 0,998420 | 298 | 0,998619 | 339 | 0,998770 |
| 258 | 0,998425 | 299 | 0,998623 | 340 | 0,998774 |
| 259 | 0,998431 | 300 | 0,998627 | 341 | 0,998777 |
| 260 | 0,998436 | 301 | 0,998632 | 342 | 0,998780 |
| 261 | 0,998442 | 302 | 0,998636 | 343 | 0,998783 |
| 262 | 0,998447 | 303 | 0,998640 | 344 | 0,998786 |
| 263 | 0,998453 | 304 | 0,998644 | 345 | 0,998790 |
| 264 | 0,998458 | 305 | 0,998648 | 346 | 0,998793 |
| 265 | 0,998463 | 306 | 0,998652 | 347 | 0,998796 |
| 266 | 0,998469 | 307 | 0,998656 | 348 | 0,998799 |
| 267 | 0,998474 | 308 | 0,998660 | 349 | 0,998802 |
| 268 | 0,998479 | 309 | 0,998664 | 350 | 0,998805 |
| 269 | 0,998484 | 310 | 0,998668 | 351 | 0,998808 |
| 270 | 0,998489 | 311 | 0,998671 | 352 | 0,998811 |
| 271 | 0,998495 | 312 | 0,998675 | 353 | 0,998814 |
| 272 | 0,998500 | 313 | 0,998679 | 354 | 0,998817 |
| 273 | 0,998505 | 314 | 0,998683 | 355 | 0,998820 |
| 274 | 0,99851 | 315 | 0,998687 | 356 | 0,998823 |
| 275 | 0,998515 | 316 | 0,998690 | 357 | 0,998826 |
| 276 | 0,998519 | 317 | 0,998694 | 358 | 0,998829 |
| 277 | 0,998524 | 318 | 0,998698 | 359 | 0,998832 |
| 278 | 0,998529 | 319 | 0,998701 | 360 | 0,998835 |
| 279 | 0,998534 | 320 | 0,998705 | 361 | 0,998837 |
| 280 | 0,998539 | 321 | 0,998709 | 362 | 0,998840 |
| 281 | 0,998544 | 322 | 0,998712 | 363 | 0,998843 |
| 282 | 0,998548 | 323 | 0,998716 | 364 | 0,998846 |
| N | c4'(N) | N | c4'(N) | N | c4'(N) |
|---|---|---|---|---|---|
| 365 | 0,998849 | 411 | 0,998963 | 457 | 0,999054 |
| 366 | 0,998851 | 412 | 0,998965 | 458 | 0,999056 |
| 367 | 0,998854 | 413 | 0,998967 | 459 | 0,999058 |
| 368 | 0,998857 | 414 | 0,998970 | 460 | 0,999060 |
| 369 | 0,998860 | 415 | 0,998972 | 461 | 0,999061 |
| 370 | 0,998862 | 416 | 0,998974 | 462 | 0,999063 |
| 371 | 0,998865 | 417 | 0,998976 | 463 | 0,999065 |
| 372 | 0,998868 | 418 | 0,998978 | 464 | 0,999067 |
| 373 | 0,998871 | 419 | 0,998980 | 465 | 0,999068 |
| 374 | 0,998873 | 420 | 0,998982 | 466 | 0,999070 |
| 375 | 0,998876 | 421 | 0,998985 | 467 | 0,999072 |
| 376 | 0,998879 | 422 | 0,998987 | 468 | 0,999073 |
| 377 | 0,998881 | 423 | 0,998989 | 469 | 0,999075 |
| 378 | 0,998884 | 424 | 0,998991 | 470 | 0,999077 |
| 379 | 0,998886 | 425 | 0,998993 | 471 | 0,999078 |
| 380 | 0,998889 | 426 | 0,998995 | 472 | 0,999080 |
| 381 | 0,998892 | 427 | 0,998997 | 473 | 0,999082 |
| 382 | 0,998894 | 428 | 0,998999 | 474 | 0,999084 |
| 383 | 0,998897 | 429 | 0,999001 | 475 | 0,999085 |
| 384 | 0,998899 | 430 | 0,999003 | 476 | 0,999087 |
| 385 | 0,998902 | 431 | 0,999005 | 477 | 0,999088 |
| 386 | 0,998904 | 432 | 0,999007 | 478 | 0,999090 |
| 387 | 0,998907 | 433 | 0,999009 | 479 | 0,999092 |
| 388 | 0,998909 | 434 | 0,999011 | 480 | 0,999093 |
| 389 | 0,998912 | 435 | 0,999013 | 481 | 0,999095 |
| 390 | 0,998914 | 436 | 0,999015 | 482 | 0,999097 |
| 391 | 0,998917 | 437 | 0,999017 | 483 | 0,999098 |
| 392 | 0,998919 | 438 | 0,999019 | 484 | 0,999100 |
| 393 | 0,998921 | 439 | 0,999021 | 485 | 0,999101 |
| 394 | 0,998924 | 440 | 0,999023 | 486 | 0,999103 |
| 395 | 0,998926 | 441 | 0,999025 | 487 | 0,999104 |
| 396 | 0,998929 | 442 | 0,999027 | 488 | 0,999106 |
| 397 | 0,998931 | 443 | 0,999028 | 489 | 0,999108 |
| 398 | 0,998933 | 444 | 0,999030 | 490 | 0,999109 |
| 399 | 0,998936 | 445 | 0,999032 | 491 | 0,999111 |
| 400 | 0,998938 | 446 | 0,999034 | 492 | 0,999112 |
| 401 | 0,998940 | 447 | 0,999036 | 493 | 0,999114 |
| 402 | 0,998943 | 448 | 0,999038 | 494 | 0,999115 |
| 403 | 0,998945 | 449 | 0,999040 | 495 | 0,999117 |
| 404 | 0,998947 | 450 | 0,999042 | 496 | 0,999118 |
| 405 | 0,998950 | 451 | 0,999043 | 497 | 0,999120 |
| 406 | 0,998952 | 452 | 0,999045 | 498 | 0,999121 |
| 407 | 0,998954 | 453 | 0,999047 | 499 | 0,999123 |
| 408 | 0,998956 | 454 | 0,999049 | 500 | 0,999124 |
| 409 | 0,998959 | 455 | 0,999051 | ||
| 410 | 0,998961 | 456 | 0,999052 |
Gamma-Tabelle
Ermitteln Sie anhand der nachfolgenden Tabelle einen Wert für γN, 1-α zum Berechnen des Konfidenzintervalls für Z.Bench, und bestimmen Sie anschließend mit der zweiten Gleichung den genauen Wert von γN, 1-α.
| 1 – α | |||||
| N | 0,800 | 0,850 | 0,900 | 0,950 | 0,990 |
| 5 | 3,544 | 4,138 | 4,961 | 6,350 | 9,750 |
| 6 | 3,485 | 4,078 | 4,903 | 6,300 | 9,636 |
| 7 | 3,443 | 4,035 | 4,861 | 6,260 | 9,567 |
| 8 | 3,413 | 4,003 | 4,829 | 6,229 | 9,520 |
| 9 | 3,390 | 3,979 | 4,804 | 6,204 | 9,484 |
| 10 | 3,372 | 3,960 | 4,783 | 6,183 | 9,457 |
| 12 | 3,345 | 3,931 | 4,753 | 6,152 | 9,416 |
| 14 | 3,326 | 3,911 | 4,732 | 6,130 | 9,387 |
| 16 | 3,312 | 3,986 | 4,716 | 6,113 | 9,365 |
| 18 | 3,301 | 3,884 | 4,703 | 6,099 | 9,348 |
| 20 | 3,293 | 3,875 | 4,693 | 6,089 | 9,335 |
| 25 | 3,278 | 3,858 | 4,675 | 6,069 | 9,310 |
| 30 | 3,268 | 3,848 | 4,664 | 6,056 | 9,294 |
| 35 | 3,261 | 3,840 | 4,655 | 6,047 | 9,282 |
| 40 | 3,255 | 3,834 | 4,649 | 6,040 | 9,274 |
| 50 | 3,248 | 3,826 | 4,640 | 6,031 | 9,262 |
| 60 | 3,243 | 3,821 | 4,634 | 6,024 | 9,253 |
| 80 | 3,237 | 3,814 | 4,627 | 6,016 | 9,244 |
| 100 | 3,233 | 3,810 | 4,623 | 6,011 | 9,238 |
| >100 | 3,219 | 3,794 | 4,605 | 5,991 | 9,210 |
Wenn N und 1 – a in der Tabelle nicht aufgeführt sind, bestimmen Sie den Wert für γN, 1-α mit der Extrapolationsmethode. Beispiel:
- Für einen Wert von α zwischen 0,05 und 0,1 (d. h. 0,95 > 1 – α > 0,90) und N = 10,
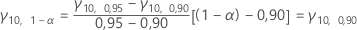
- Für einen Wert von N zwischen 60 und 80 sowie α = 0,80,
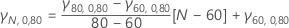
- Verwenden Sie für einen Wert von α zwischen 0,05 und 0,1 sowie einen Wert von N zwischen 60 und 80 die erste Gleichung, um die Werte von γ80, 1 -α und γ60, 1-α zu berechnen.
