Z.USG, Z.OSG und Z.Bench für die potenzielle Prozessfähigkeit (innerhalb)
Benchmark-Z-Statistiken für die potenzielle Prozessfähigkeit werden berechnet, indem der Z-Wert auf der Grundlage der Standardnormalverteilung (0;1) für die entsprechenden Statistiken ermittelt wird.



Dabei gilt Folgendes:


Notation
| Begriff | Beschreibung |
|---|---|
| Φ (X) | Kumulative Verteilungsfunktion (CDF) einer Standardnormalverteilung |
| Φ-1 (X) | Inverse CDF einer Standardnormalverteilung |
 | Standardabweichung innerhalb von Teilgruppen |
Konfidenzintervalle für Z.Bench für einen Prozess mit zwei Spezifikationsgrenzen
Beidseitiges Intervall


Dabei gilt Folgendes:
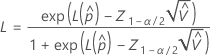
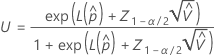
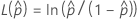

So berechnen Sie  , die Stichprobenschätzungen durch die Parameter in der Formel für
, die Stichprobenschätzungen durch die Parameter in der Formel für 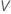 :
:



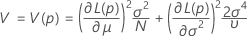
Dabei gilt Folgendes:
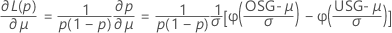
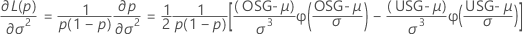
Einseitige obere Konfidenzgrenze
Um eine einseitige obere Konfidenzgrenze zu berechnen, ändern Sie 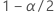 An
An  in der Definition von U.
in der Definition von U.
Notation
| Begriff | Beschreibung |
|---|---|
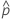 | geschätzte Wahrscheinlichkeiten für den Randbereich außerhalb der Spezifikationsgrenzen |
 | das (1 - α / 2)tes Perzentil der Standardnormalverteilung |
| α | Alpha für das Konfidenzniveau |
 | Prozessmittelwert (aus den Stichprobendaten geschätzt oder ein historischer Wert) |
| s | Standardabweichung innerhalb der Teilgruppen |
| υ | Freiheitsgrade für s |
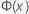 | kumulative Verteilungsfunktion (CDF) einer Standardnormalverteilung |
 | die Wahrscheinlichkeitsdichtefunktion (PDF) aus einer Standardnormalverteilung |
| OSG | obere Spezifikationsgrenze |
| USG | untere Spezifikationsgrenze |
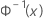 | inverse kumulative Verteilungsfunktion einer Standardnormalverteilung |
Konfidenzintervalle für Z.Bench für einen Prozess mit einer Spezifikationsgrenze
Die Berechnungen für das Konfidenzintervall für Z.Bench hängen davon ab, welche Spezifikationsgrenze für den Prozess vorhanden ist.
Untere Spezifikationsgrenze, beidseitiges Konfidenzintervall
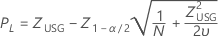
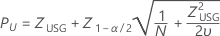

Untere Spezifikationsgrenze, einseitige Konfidenzgrenze

Minitab löst die folgende Gleichung, um p1zu ermitteln:
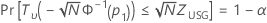
Dabei gilt Folgendes:

Obere Spezifikationsgrenze, beidseitiges Konfidenzintervall
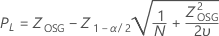
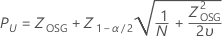

Obere Spezifikationsgrenze, einseitige Konfidenzgrenze

Minitab löst die folgende Gleichung, um p2zu ermitteln:
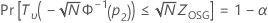
Dabei gilt Folgendes:

Notation
| Begriff | Beschreibung |
|---|---|
| USG | untere Spezifikationsgrenze |
| OSG | obere Spezifikationsgrenze |
| α | Alpha für das Konfidenzniveau |
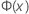 | kumulative Verteilungsfunktion (CDF) einer Standardnormalverteilung |
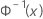 | inverse kumulative Verteilungsfunktion einer Standardnormalverteilung |
 | (1 – α/2)-tes Perzentil der Standardnormalverteilung |
| N | Gesamtzahl der Messwerte |
| υ | Freiheitsgrade für s |
 | Prozessmittelwert (aus den Stichprobendaten geschätzt oder ein historischer Wert) |
| s | Standardabweichung innerhalb der Teilgruppen |
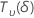 | eine Zufallsvariable, die als nicht-zentrale t-Verteilung mit  Freiheitsgrade und Nichtzentralitätsparameter δ Freiheitsgrade und Nichtzentralitätsparameter δ |
