In diesem Thema
PPM < USG für beobachtete Leistung
Die Anzahl der Teile pro Million, deren Messwerte die untere Spezifikationsgrenze unterschreiten, wird wie folgt berechnet:
Notation
| Begriff | Beschreibung |
|---|---|
| USG | Untere Spezifikationsgrenze |
| N | Gesamtzahl der Beobachtungen |
PPM > OSG für beobachtete Leistung
Die Anzahl der Teile pro Million, deren Messwerte die obere Spezifikationsgrenze überschreiten, wird wie folgt berechnet:
Notation
| Begriff | Beschreibung |
|---|---|
| OSG | Obere Spezifikationsgrenze |
| N | Gesamtzahl der Beobachtungen |
PPM gesamt für beobachtete Leistung
Die Gesamtzahl der Teile pro Million, die außerhalb der Spezifikationsgrenzen liegen, wird wie folgt berechnet:
Notation
| Begriff | Beschreibung |
|---|---|
| USG | Untere Spezifikationsgrenze |
| OSG | Obere Spezifikationsgrenze |
| N | Gesamtzahl der Beobachtungen |
Konfidenzintervalle für PPM und % außerhalb der Spezifikation
Die Berechnung des Konfidenzintervalls ist für PPM und Prozent identisch, mit Ausnahme eines Schritts am Ende, um das Ergebnis in die richtigen Einheiten umzurechnen. Die folgenden Formeln gelten für die beidseitige 100(1 – 
)%-Konfidenzintervalle. Um einseitige Konfidenzintervalle zu finden, ersetzen Sie 
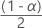mit (1 – 
).
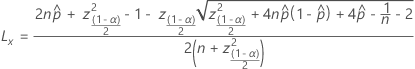
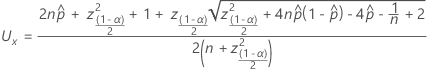
Um das Ergebnis der Formel in PPM umzuwandeln, multiplizieren Sie es mit 1.000.000.
Um das Ergebnis der Formel in einen Prozentsatz umzuwandeln, multiplizieren Sie mit 100.
Wenn keine beobachteten Einheiten außerhalb einer Spezifikationsgrenze liegen, ist die untere Konfidenzgrenze 0. Wenn alle beobachteten Einheiten außerhalb einer Spezifikationsgrenze liegen, ist die obere Konfidenzgrenze 1.
Notation
| Begriff | Beschreibung |
|---|---|
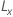 | Untere Konfidenzgrenze |
 | Obere Konfidenzgrenze |
| n | Gesamtanzahl der Einheiten |
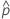 | Empirische Wahrscheinlichkeit, dass eine Einheit außerhalb der Spezifikation liegt: fehlerhaft / gesamt. |
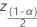 | (1 –  )/2 Perzentil aus einer Standardnormalverteilung |
 | 1 – Das Konfidenzniveau |
Literaturhinweise
Newcombe, R. G. (1998). Two-sided confidence intervals for the single proportion: comparison of seven methods. Statistics in Medicine, 17(8), 857-872.
Tong, L. I., & Chen, J. P. (1998). Lower confidence limits of process capability indices for nonnormal process distributions. International Journal of Quality & Reliability Management, 15(8/9), 907-919.
