In diesem Thema
ML-Schätzwerte der Verteilungsparameter
Bei der Maximum-Likelihood-Methode (ML) werden die Werte der Verteilungsparameter geschätzt, die die Likelihood-Funktion für jede Verteilung maximieren. Ziel ist es, die beste Übereinstimmung zwischen dem Verteilungsmodell und den beobachteten Stichprobendaten zu erhalten.
- Teststelle
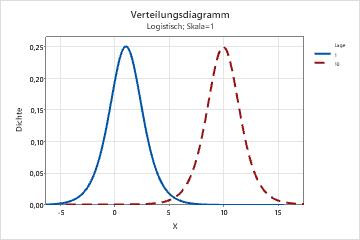
- Dieser Parameter wirkt sich auf die Lage einer Verteilung aus. Mit verschiedenen Lageparametern wird zum Beispiel eine logistische Verteilung entlang der horizontalen Achse verschoben.
- Form
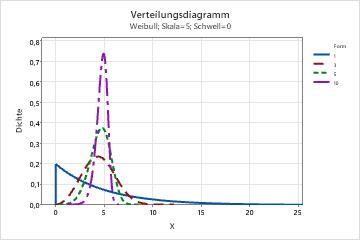
- Dieser Parameter wirkt sich auf die Form der Verteilung aus. Mit verschiedenen Formparametern erscheint zum Beispiel eine Weibull-Verteilung schiefer oder symmetrischer.
- Skala
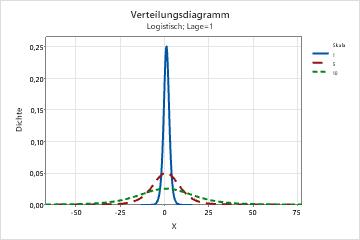
- Dieser Parameter wirkt sich auf die Skala der Verteilung aus. Mit verschiedenen Skalenparametern erscheint zum Beispiel eine logistische Verteilung „gedehnter oder komprimierter.
- Schwellenwert
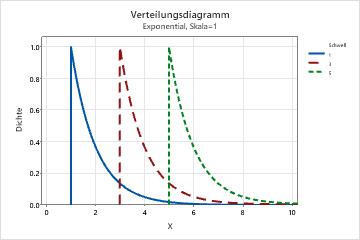
- Dieser Parameter wirkt sich auf das Minimum einer Zufallsvariable aus. Mit verschiedenen Schwellenwertparametern wird zum Beispiel eine Exponentialverteilung für einen anderen Wertebereich definiert.
Hinweis
Minitab verwendet die Maximum-Likelihood-Methode zum Berechnen der Parameterschätzwerte für alle Verteilungen mit Ausnahme der Normalverteilung und der lognormalen Verteilung, für die stattdessen erwartungstreue Parameterschätzwerte verwendet werden.
Interpretation
Verwenden Sie die ML-Schätzwerte der Verteilungsparameter, um das für Ihre Daten verwendete spezifische Verteilungsmodell besser zu verstehen. Angenommen, ein Qualitätstechniker bestimmt auf der Grundlage des historischen Prozesswissens sowie der Anderson-Darling- und LVT-p-Werte, dass die Weibull-Verteilung mit 3 Parametern die beste Anpassung für die Prozessdaten bietet. Um die spezifische Weibull-Verteilung mit 3 Parametern zu verstehen, die zum Modellieren der Daten verwendet wird, untersucht der Techniker die ML-Schätzwerte für Form, Skala und Schwellenwert, die für die Verteilung berechnet wurden.
Verteilung
Die Analyse liefert Statistiken zur Güte der Anpassung und Verteilungsparameter für mehrere häufig verwendete Verteilungen. Viele dieser Verteilungen sind vielseitig und können eine Reihe von stetigen Daten modellieren, darunter Daten mit positiven Werten, negativen Werten und 0.
- Lognormal
- Exponential
- Weibull
- Gamma
- Loglogistisch
Wenn Ihre Daten daher negative Werte oder 0 enthalten, gibt Minitab für diese speziellen Verteilungen keine Ergebnisse aus. Verwenden Sie in diesem Fall die Ergebnisse für die jeweilige Version der Verteilung mit mehr Parametern. Wenn die Daten z. B. negative Werte enthalten, meldet Minitab keine Ergebnisse für die Lognormalverteilung. Verwenden Sie stattdessen die Ergebnisse für die lognormale Verteilung mit 3 Parametern.
Weitere Informationen zu den Distributionen finden Sie unter Weshalb ist Weibull-Verteilung die Standardverteilung für die Prozessfähigkeitsanalyse für nicht normalverteilte Daten?.
Hinweis
Informationen zu den Formeln, mit denen PDF und CDF für die einzelnen Verteilungen berechnet werden, finden Sie unter Methoden und Formeln für Verteilungen in Identifikation der Verteilung.
P
Hinweis
Für die Verteilungen mit 3 Parametern (mit Ausnahme der Weibull-Verteilung) sind keine p-Werte für den AD-Test verfügbar.
Interpretation
Verwenden Sie den p-Wert, um die Anpassung der Verteilung zu beurteilen.
- P ≤ α: Die Daten folgen nicht der Verteilung (Ablehnen H0)
- Wenn der p-Wert kleiner oder gleich dem Signifikanzniveau ist, weisen Sie die Nullhypothese zurück und schlussfolgern, dass die Daten der Verteilung nicht folgen.
- P > α: Es kann nicht geschlossen werden, dass die Daten nicht der Verteilung folgen (H0kann nicht abgelehnt werden)
- Wenn der p-Wert größer als das Signifikanzniveau ist, weisen Sie die Nullhypothese nicht zurück. Es liegen nicht genügend Anzeichen dafür vor, dass die Daten der Verteilung nicht folgen. Sie können annehmen, dass die Daten der Verteilung folgen.
- Wählen Sie die Verteilung aus, die in Ihrer Branche oder Anwendung am gängigsten ist.
- Wählen Sie die Verteilung aus, die die konservativsten Ergebnisse liefert. Sie können beispielsweise eine Prozessfähigkeitsanalyse mit verschiedenen Verteilungen durchführen und anschließend die Verteilung auswählen, die die konservativsten Prozessfähigkeitsindizes liefert. Weitere Informationen erhalten Sie, wenn Sie Verteilungsperzentile für Identifikation der Verteilung auf "Prozente und Perzentile" klicken.
- Wählen Sie die einfachste Verteilung aus, die eine gute Anpassung an die Daten bietet. Wenn beispielsweise sowohl eine Verteilung mit 2 Parametern als auch eine Verteilung mit 3 Parametern eine gute Anpassung bieten, könnten Sie die einfachere Verteilung mit 2 Parametern auswählen.
Wichtig
Seien Sie beim Interpretieren von Ergebnissen, die aus sehr kleinen oder sehr großen Stichproben stammen, vorsichtig. Bei einer sehr kleinen Stichprobe besitzt ein Test der Anpassungsgüte möglicherweise nicht die erforderliche Trennschärfe, um signifikante Abweichungen von der Verteilung zu erkennen. Bei einer sehr großen Stichprobe hingegen ist die Trennschärfe so groß, dass auch kleine Abweichungen von der Verteilung erkannt werden, die keine praktische Bedeutung besitzen. Verwenden Sie zusätzlich zu den p-Werten die Wahrscheinlichkeitsnetze, um die Verteilungsanpassung zu beurteilen.
Ergebnisse der automatisierten Funktionsverteilung: Kalzium
| Verteilung | Lage | Skala | Schwellenwert | Form | P | Ppk |
|---|---|---|---|---|---|---|
| Normal | 50,7820 | 2,7648 | 0,0463827 | 1,2999 | ||
| Weibull | 52,1368 | 17,825 | <0,01 | 0,7907 | ||
| Lognormal* | 3,9261 | 0,0537 | 0,0848247 | 1,4732 | ||
| Kleinster Extremwert | 52,2226 | 2,9589 | <0,01 | 0,7153 | ||
| Größter Extremwert | 49,5037 | 2,1699 | >0,25 | |||
| Gamma | 0,1447 | 351,044 | 0,0706812 | 1,4275 | ||
| Logistisch | 50,5718 | 1,5948 | 0,0339831 | 1,0023 | ||
| Loglogistisch | 3,9226 | 0,0312 | 0,0495201 | 1,0864 | ||
| Exponential | 50,7820 | <0,0025 | -0,0378 | |||
| Weibull mit 3 Parametern | 4,5365 | 46,6658 | 1,476 | >0,5 | ||
| Lognormal mit 3 Parametern | 1,6930 | 0,4685 | 44,7401 | |||
| Gamma mit 3 Parametern | 1,6370 | 45,8838 | 2,992 | |||
| Loglogistisch mit 3 Parametern | 1,5486 | 0,3276 | 45,4618 | |||
| Exponential mit 2 Parametern | 4,0633 | 46,7187 | 0,0140796 | |||
| Box-Cox-Transformation | 0,0000 | 0,0000 | 0,324445 | 2,5062 | ||
| Johnson-Transformation | 0,0290 | 0,9729 | 0,985835 | 2,7129 | ||
| Nichtparametrisch | 2,8889 |
| Verteilung | Cpk |
|---|---|
| Normal | 1,3504 |
| Weibull | |
| Lognormal* | |
| Kleinster Extremwert | |
| Größter Extremwert | |
| Gamma | |
| Logistisch | |
| Loglogistisch | |
| Exponential | |
| Weibull mit 3 Parametern | |
| Lognormal mit 3 Parametern | |
| Gamma mit 3 Parametern | |
| Loglogistisch mit 3 Parametern | |
| Exponential mit 2 Parametern | |
| Box-Cox-Transformation | 2,5335 |
| Johnson-Transformation | |
| Nichtparametrisch |
In diesen Ergebnissen ist die Lognormalverteilung die erste Methode, die die Daten auf dem Signifikanzniveau 0,05 anpasst. Andere Verteilungen und Transformationen bieten ebenfalls eine adäquate Anpassung an die Daten. Überlegen Sie, ob eine dieser alternativen Methoden besser mit dem Prozess kompatibel ist.
Hinweis
Bei einer Reihe von Verteilungen zeigt Minitab außerdem die Ergebnisse für die betreffende Verteilung mit einem zusätzlichen Parameter an. Zum Beispiel zeigt Minitab für die lognormale Verteilung die Ergebnisse für die Verteilung mit 2 Parametern und mit 3 Parametern an. Überlegen Sie bei Verteilungen mit zusätzlichen Parametern, ob der zusätzliche Parameter mit dem kompatibel ist, was Sie über den Prozess wissen. Wenn der Prozess z. B. eine physische Grenze bei einem Wert ungleich Null hat, ist eine Verteilung mit einem Schwellenwertparameter mit dem Prozess kompatibel.
Ppk
- Der Abstand vom Prozessmittelwert zur nächstgelegenen Spezifikationsgrenze (OSG oder USG)
- Die einseitige Streubreite des Prozesses (die 3σ-Streuung) auf der Grundlage seiner Gesamtstreuung
Interpretation
Mit Ppk können Sie die Gesamtprozessfähigkeit Ihres Prozesses auf der Grundlage von Prozesslage und Prozessstreubreite auswerten. Die Gesamtprozessfähigkeit gibt die tatsächliche Leistung Ihres Prozesses an, die der Kunde über die Zeit wahrnimmt.
Im Allgemeinen verweisen höhere Ppk-Werte auf einen fähigeren Prozess. Niedrigere Ppk-Werte geben an, dass der Prozess möglicherweise verbessert werden muss.
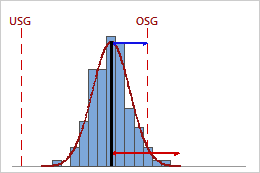
Niedriger Ppk
In diesem Beispiel ist der Abstand vom Prozessmittelwert zur nächstgelegenen Spezifikationsgrenze (OSG) kleiner als die einseitige Prozessstreubreite. Daher ist Ppk niedrig (0,66), und die Gesamtprozessfähigkeit des Prozesses ist schlecht.
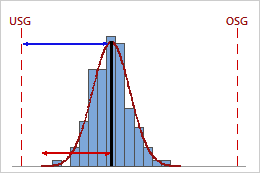
Hoher Ppk
In diesem Beispiel ist der Abstand vom Prozessmittelwert zur nächstgelegenen Spezifikationsgrenze (USG) größer als die einseitige Prozessstreubreite. Daher ist Ppk hoch (1,68), und die Gesamtprozessfähigkeit des Prozesses ist gut.
-
Vergleichen Sie Ppk mit einem Benchmark-Wert, der den Minimalwert darstellt, der für den Prozess akzeptabel ist. In vielen Branchen wird der Benchmark-Wert 1,33 verwendet. Wenn Ppk niedriger als der Benchmark-Wert ist, erwägen Sie Maßnahmen zur Verbesserung Ihres Prozesses.
-
Vergleichen Sie Pp und Ppk. Wenn Pp und Ppk annähernd übereinstimmen, ist der Prozess genau zwischen den Spezifikationsgrenzen zentriert. Wenn sich Pp und Ppk unterscheiden, ist der Prozess nicht zentriert.
-
Vergleichen Sie Ppk und Cpk. Wenn ein Prozess statistisch beherrscht ist, sind Ppk und Cpk annähernd gleich. Die Differenz zwischen Ppk und Cpk stellt die Verbesserung der Prozessfähigkeit dar, die Sie erwarten können, wenn alle Shifts und Drifts im Prozess beseitigen würden.
Vorsicht
Der Ppk-Index stellt nur eine Seite der Prozesskurve dar und gibt keinen Aufschluss über die Leistung des Prozesses auf der anderen Seite der Prozesskurve.
Die folgenden Grafiken zeigen beispielsweise zwei Prozesse mit identischen Ppk-Werten. Ein Prozess verletzt jedoch beide Spezifikationsgrenzen, während der andere Prozess nur die obere Spezifikationsgrenze verletzt.
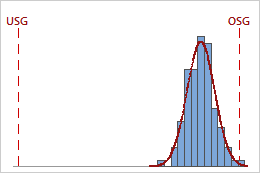
Ppk = Min {PPL = 4,01; PPU = 0,64} = 0,64
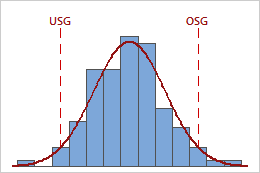
Ppk = PPL = PPU = 0,64
Wenn Ihr Prozess unzulängliche Teile produziert, die jenseits beider Spezifikationsgrenzen liegen, erwägen Sie, andere Indizes zu verwenden (z. B. Z.Bench), um die Prozessfähigkeit umfassender zu beurteilen.
Cpk
- Der Abstand vom Prozessmittelwert zur nächstgelegenen Spezifikationsgrenze (OSG oder USG)
- Die einseitige Streubreite des Prozesses (die 3σ-Streuung) auf der Grundlage der Standardabweichung innerhalb von Teilgruppen
Interpretation
Mit Cpk können Sie die potenzielle Prozessfähigkeit Ihres Prozesses auf der Grundlage von Prozesslage und Prozessstreubreite auswerten. Die potenzielle Prozessfähigkeit gibt die Prozessfähigkeit an, die erzielt werden könnte, wenn Shifts und Drifts im Prozess beseitigt würden.
Im Allgemeinen verweisen höhere Cpk-Werte auf einen fähigeren Prozess. Niedrigere Cpk-Werte geben an, dass der Prozess möglicherweise verbessert werden muss.
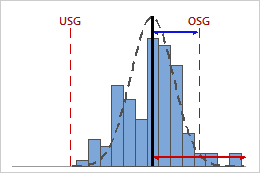
Niedriger Cpk
In diesem Beispiel ist der Abstand vom Prozessmittelwert zur nächstgelegenen Spezifikationsgrenze (OSG) kleiner als die einseitige Prozessstreubreite. Daher ist Cpk niedrig (0,80), und die potenzielle Prozessfähigkeit des Prozesses ist schlecht.
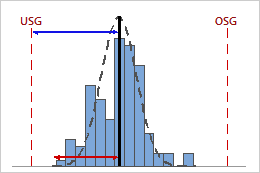
Hoher Cpk
In diesem Beispiel ist der Abstand vom Prozessmittelwert zur nächstgelegenen Spezifikationsgrenze (USG) größer als die einseitige Prozessstreubreite. Daher ist Cpk hoch (1,64), und die potenzielle Prozessfähigkeit des Prozesses ist gut.
Sie können Cpk mit anderen Werten vergleichen, um weitere Informationen zur Prozessfähigkeit Ihres Prozesses zu erhalten.
-
Vergleichen Sie Cpk mit einem Benchmark-Wert, der den Minimalwert darstellt, der für den Prozess akzeptabel ist. In vielen Branchen wird der Benchmark-Wert 1,33 verwendet. Wenn Cpk niedriger als der Benchmark-Wert ist, erwägen Sie Maßnahmen zur Verbesserung Ihres Prozesses, z. B. die Verringerung seiner Streuung oder einen Shift seiner Lage.
-
Vergleichen Sie Cp und Cpk. Wenn Cp und Cpk annähernd übereinstimmen, ist der Prozess genau zwischen den Spezifikationsgrenzen zentriert. Wenn sich Cp und Cpk unterscheiden, ist der Prozess nicht zentriert.
-
Vergleichen Sie Ppk und Cpk. Wenn ein Prozess statistisch beherrscht ist, sind Ppk und Cpk annähernd gleich. Die Differenz zwischen Ppk und Cpk stellt die Verbesserung der Prozessfähigkeit dar, die Sie erwarten können, wenn alle Shifts und Drifts im Prozess beseitigen würden.
Vorsicht
Der Cpk-Index stellt nur eine Seite der Prozesskurve dar und gibt keinen Aufschluss über die Leistung des Prozesses auf der anderen Seite der Prozesskurve.
Die Grafiken unten bilden beispielsweise Prozesse mit identischen Cpk-Werten ab. Ein Prozess verletzt jedoch beide Spezifikationsgrenzen, während der andere Prozess nur die obere Spezifikationsgrenze verletzt.
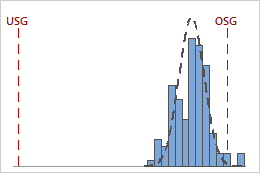
Cpk = Min {CPL = 4,58; CPU = 0,93} = 0,93
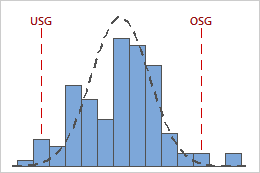
Cpk = CPL = CPU = 0,93
Wenn Ihr Prozess unzulängliche Teile produziert, die jenseits beider Spezifikationsgrenzen liegen, erwägen Sie, andere Indizes zu verwenden (z. B. Z.Bench), um die Prozessfähigkeit umfassender zu beurteilen.
Cnpk
Cnpk ist ein Maß für die Gesamtfähigkeit des Prozesses und entspricht dem Minimum von Cnpu und Cnpl.
- Die einseitige Spezifikationsspanne, vom Prozessmedian bis zur oberen Spezifikationsgrenze
- Die Hälfte der Prozessstreuung, vom Prozessmedian bis zur Schätzung des oberen Endes des Prozesses
- Die einseitige Spezifikationsspanne, vom Prozessmedian bis zur unteren Spezifikationsgrenze
- Die Hälfte der Prozessstreuung, vom Prozessmedian bis zur Schätzung des unteren Endes des Prozesses
Interpretation
Verwenden Sie Cnpk, um die Gesamtfähigkeit Ihres Prozesses sowohl auf der Grundlage des Prozessstandorts als auch der Prozessstreuung zu bewerten. Die Gesamtprozessfähigkeit gibt die tatsächliche Leistung Ihres Prozesses an, die der Kunde über die Zeit wahrnimmt.
Im Allgemeinen weisen höhere Cnpk-Werte auf einen leistungsfähigeren Prozess hin. Niedrigere Cnpk-Werte weisen darauf hin, dass Ihr Prozess möglicherweise verbessert werden muss.
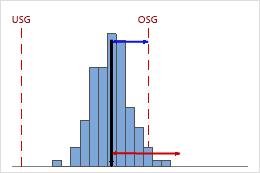
Niedriger Cnpk
In diesem Beispiel ist die Leistung des Prozesses hinsichtlich der oberen Spezifikationsgrenze schlechter als hinsichtlich der unteren Spezifikationsgrenze. Der Cnpk-Wert entspricht Cnpu (≈ 0,40), was niedrig ist und auf eine schlechte Prozessfähigkeit hinweist.
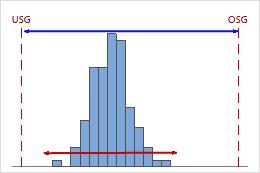
Hoher Cnpk
In diesem Beispiel ist die Leistung des Prozesses hinsichtlich der unteren Spezifikationsgrenze schlechter als hinsichtlich der oberen Spezifikationsgrenze. Der Cnpk-Wert entspricht Cnpl (≈ 1,40), was hoch ist und auf eine gute Prozessfähigkeit hinweist.
-
Wenn Cnpk < 1, then the specification spread is less than the process spread.
-
Vergleichen Sie Cnpk mit einem Benchmarkwert, der den Mindestwert darstellt, der für Ihren Prozess akzeptabel ist. In vielen Branchen wird der Benchmark-Wert 1,33 verwendet. Wenn der Cnpk niedriger als Ihr Benchmark ist, sollten Sie Möglichkeiten zur Verbesserung Ihres Prozesses in Betracht ziehen.
Achtung
Der Cnpk-Index stellt die Prozessfähigkeit nur für die „schlechtere“ Seite der Prozessmesswerte dar, d. h. die Seite, bei der die Prozessleistung geringer ist. Wenn der Prozess unzulängliche Teile erzeugt, die zu beiden Seiten der Spezifikationsgrenzen liegen, prüfen Sie die Prozessfähigkeitsgrafiken und die Wahrscheinlichkeit, dass Teile außerhalb beider Spezifikationsgrenzen liegen, um die Prozessfähigkeit eingehender zu untersuchen.
