Qualitätstechniker in einem Unternehmen, das Bodenfliesen herstellt, untersuchen Kundenbeschwerden in Bezug auf eine Wölbung von Fliesen. Um die Qualität der Produktion sicherzustellen, messen die Techniker die Wölbung in 10 Bodenfliesen an jedem Arbeitstag über 10 Tage. Die obere Spezifikationsgrenze für die Verzugsmessung liegt bei 6 mm. Die Ingenieure wollen verschiedene Optionen ausloten, um eine vernünftige Methode zu finden, um die Leistungsfähigkeit des Prozesses abzuschätzen.
- Öffnen Sie die Beispieldaten Fliesenwölbung.MWX.
- Wählen Sie
- Geben Sie im Feld Einzelne Spalte die Spalte Wölbung ein.
- Geben Sie im Feld Teilgruppengröße den Wert 10 ein.
- Geben Sie im Feld Obere Spezifikationsgrenze den Wert 6 ein.
- Wählen Sie OK aus.
Interpretieren der Ergebnisse
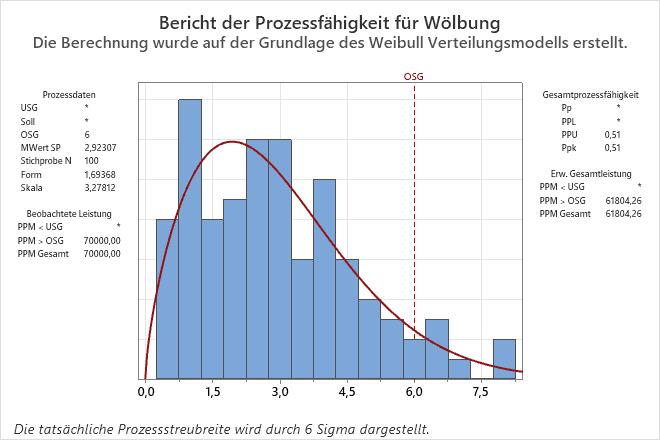
Die Analyse zeigt einen Prozessfähigkeitsbericht für die erste Methode an, die eine angemessene Anpassung bietet. Für die Verformung der Kacheln wird in den Ergebnissen eine Weibull-Verteilung verwendet.
Bei diesen Daten scheinen die Messungen am rechten Ende des Histogramms über der oberen Spezifikationsgrenze zu liegen. Daher überschreitet die Wölbung der Fliesen häufig die obere Spezifikationsgrenze von 6 mm. Die beobachteten PPM > OSG verweisen darauf, dass 70.000 Fliesen pro Million über der oberen Spezifikationsgrenze liegen. Der Ppk (gesamt) beträgt 0,51 und liegt damit unter dem allgemein anerkannten Branchenrichtwert 1,33. Daher schlussfolgern die Techniker, dass der Prozess nicht fähig ist und die Kundenanforderungen nicht erfüllt.
Die Tabelle der Verteilungsergebnisse zeigt die Reihenfolge der Auswertung der Methoden. In der ersten Zeile lautet die Schlussfolgerung für den Anderson-Darling-Test, dass die Daten keiner Normalverteilung auf dem Signifikanzniveau von 0,05 folgen, da der p-Wert kleiner als 0,05 ist. In der zweiten Zeile lautet die Schlussfolgerung für den Anderson-Darling-Test, dass die Weibull-Verteilung angemessen an die Daten angepasst ist, da der p-Wert größer als 0,05 ist. Die Prozessfähigkeitsergebnisse beziehen sich auf die Weibull-Verteilung, da die Weibull-Verteilung die erste Methode in der Liste ist, die eine vernünftige Anpassung bietet.
Die Ingenieure nutzen das Prozesswissen, um zu überlegen, ob die Weibull-Verteilung eine sinnvolle Wahl ist. Beispielsweise hat die Weibull-Verteilung einen Rand bei 0. In den Daten ist 0 eine Grenze, die eine nicht verzerrte Kachel darstellt.
Ergebnisse der automatisierten Funktionsverteilung: Wölbung
| Verteilung | Lage | Skala | Schwellenwert | Form | P | Ppk |
|---|---|---|---|---|---|---|
| Normal | 2,9231 | 1,7860 | 0,0100421 | 0,5743 | ||
| Weibull* | 3,2781 | 1,6937 | >0,25 | 0,5133 | ||
| Lognormal | 0,8443 | 0,7444 | <0,005 | 0,4242 | ||
| Kleinster Extremwert | 3,8641 | 1,9924 | <0,01 | 0,5362 | ||
| Größter Extremwert | 2,0958 | 1,4196 | 0,212835 | 0,5130 | ||
| Gamma | 1,2477 | 2,3428 | 0,238337 | 0,4851 | ||
| Logistisch | 2,7959 | 1,0162 | 0,0127347 | 0,5799 | ||
| Loglogistisch | 0,9097 | 0,4217 | <0,005 | 0,4090 | ||
| Exponential | 2,9231 | <0,0025 | 0,3780 | |||
| Weibull mit 3 Parametern | 2,9969 | 0,2099 | 1,5049 | 0,467097 | 0,4980 | |
| Lognormal mit 3 Parametern | 1,3788 | 0,4184 | -1,4002 | 0,4961 | ||
| Gamma mit 3 Parametern | 1,2314 | -0,0197 | 2,3898 | 0,4864 | ||
| Loglogistisch mit 3 Parametern | 1,3043 | 0,2700 | -1,0940 | 0,4656 | ||
| Exponential mit 2 Parametern | 2,6679 | 0,2552 | <0,01 | 0,3982 | ||
| Box-Cox-Transformation | 1,6237 | 0,5380 | 0,574337 | 0,5116 | ||
| Johnson-Transformation | 0,0112 | 0,9949 | 0,798895 | 0,4959 | ||
| Nichtparametrisch | 0,6187 |
| Verteilung | Cpk |
|---|---|
| Normal | 0,5838 |
| Weibull* | |
| Lognormal | |
| Kleinster Extremwert | |
| Größter Extremwert | |
| Gamma | |
| Logistisch | |
| Loglogistisch | |
| Exponential | |
| Weibull mit 3 Parametern | |
| Lognormal mit 3 Parametern | |
| Gamma mit 3 Parametern | |
| Loglogistisch mit 3 Parametern | |
| Exponential mit 2 Parametern | |
| Box-Cox-Transformation | 0,5214 |
| Johnson-Transformation | |
| Nichtparametrisch |
