Was ist die Poisson-Verteilung?
Die Poisson-Verteilung wird durch einen Parameter definiert: Lambda (λ). Dieser Parameter ist gleich dem Mittelwert und der Varianz. Wenn Lambda ausreichend große Werte aufweist, kann die Poisson-Verteilung näherungsweise mit der Normalverteilung (λ; λ) geschätzt werden.
Verwenden Sie die Poisson-Verteilung, um zu beschreiben, wie häufig ein Ereignis in einem endlichen Beobachtungsraum eintritt. Mit einer Poisson-Verteilung kann beispielsweise die Anzahl der Fehler im mechanischen System eines Flugzeugs oder die Anzahl der Anrufe in einem Callcenter pro Stunde beschrieben werden. Die Poisson-Verteilung kommt häufig in der Qualitätskontrolle, in Zuverlässigkeits- und Lebensdaueranalysen sowie im Versicherungswesen zur Anwendung.
- Die Daten sind Ereignishäufigkeiten (nicht negative ganze Zahlen ohne Obergrenze).
- Alle Ereignisse sind unabhängig voneinander.
- Die durchschnittliche Ereignisrate ändert sich über den relevanten Zeitraum nicht.
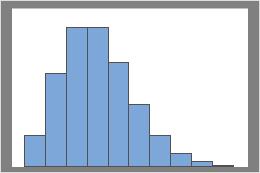
Lambda = 3
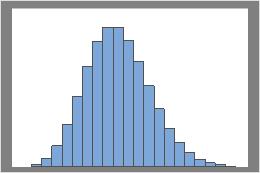
Lambda = 10
Was ist die Ereignisrate?
Die Ereignisrate ist gleich dem Mittelwert (λ) dividiert durch die Dimension des Beobachtungsraums. Sie empfiehlt sich zum Vergleichen von Poisson-Zählungen, die in unterschiedlichen Beobachtungsräumen erfasst wurden. Angenommen, Telefonzentrale A erhält 50 Anrufe in 5 Stunden und Telefonzentrale B 80 Anrufe in 10 Stunden. Sie können diese Werte nicht direkt vergleichen, da die Beobachtungsräume unterschiedlich sind. Um diese Zählungen zu vergleichen, müssen Sie die Ereignisrate berechnen. Die Rate für Telefonzentrale A lautet (50 Anrufe/5 Stunden) = 10 Anrufe/Stunde. Die Rate für Telefonzentrale B ist (80 Anrufe/10 Stunden) = 8 Anrufe/Stunde.
Unterschiede zwischen der Poisson-Verteilung und der Binomialverteilung
Die Poisson-Verteilung ähnelt der Binomialverteilung, da beide Verteilungen Ereigniszahlen modellieren. Innerhalb des endlichen Beobachtungsraums wird bei der Poisson-Verteilung jedoch keine Obergrenze für diese Anzahl festgelegt: Eine Telefonzentrale könnte eine unendliche Anzahl von Anrufen pro Tag erhalten, ohne die Anforderungen der Poisson-Verteilung zu verletzen. Umgekehrt besteht bei der Binomialverteilung eine Obergrenze für die Anzahl: Die beobachtete Anzahl der Ereignisse darf nicht größer als die Anzahl der durchgeführten Versuche sein.
