Beim Durchführen eines Experiments mit nur zwei Ergebnissen stellt die geometrische Verteilung eine diskrete Verteilung dar, mit der die Anzahl der aufeinander folgenden Versuche modelliert werden kann, die zum erstmaligen Beobachten des gewünschten Ergebnisses erforderlich sind. Darüber hinaus kann mit der geometrischen Verteilung auch die Anzahl der Nicht-Ereignisse modelliert werden, die vor dem Beobachten des ersten Ereignisses auftreten.
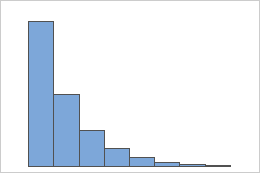
Was bedeutet „Erinnerungslosigkeit“?
Eine wichtige Eigenschaft der geometrischen Verteilung ist ihre „Erinnerungslosigkeit“. Die Wahrscheinlichkeit eines Ereignisses hängt nicht von vergangenen Versuchen ab. Daher bleibt die Ereignisrate konstant.
„Erinnerungslosigkeit“ bedeutet, dass die verbleibende Lebensdauer einer Komponente unabhängig von ihrem gegenwärtigen Alter ist. Die Eigenschaft der Erinnerungslosigkeit wird z. B. durch zufällige Versuche eines Münzwurfs demonstriert. Im Gegensatz dazu ist ein System, das dem Verschleiß unterliegt und daher mit steigender Lebensdauer eine höhere Ausfallwahrscheinlichkeit hat, nicht „erinnerungslos“.
