Verwenden Sie die Exponentialverteilung, um die Zeit zwischen Ereignissen in einem stetigen Poisson-Prozess zu modellieren. Es wird davon ausgegangen, dass unabhängige Ereignisse mit einer konstanten Rate auftreten.
Diese Verteilung dient einer Vielzahl von Anwendungen, beispielsweise für Zuverlässigkeitsanalysen für Produkte und Systeme, Warteschlangentheorie und Markov-Ketten.
- Dauer bis zum Ausfall elektronischer Komponenten
- Zeitintervall zwischen dem Eintreffen von Kunden an einem Terminal
- Zeit bis zur Beratung von Kunden in der Warteschlange
- Zeit bis zum Eintreten von Zahlungsverzug (Modellierung des Kreditrisikos)
- Zeit bis zum Zerfall eines radioaktiven Atomkerns
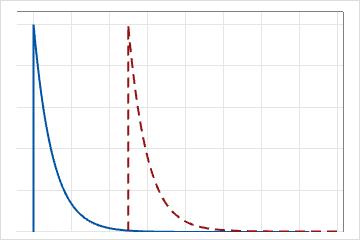
Für die Exponentialverteilung mit 1 Parameter ist der Schwellenwert 0, und die Verteilung wird durch ihren Skalenparameter definiert. Bei der Exponentialverteilung mit 1 Parameter ist der Skalenparameter gleich dem Mittelwert.
Was bedeutet „Erinnerungslosigkeit“?
Die Exponentialverteilung zeichnet sich durch die wichtige Eigenschaft der „Erinnerungslosigkeit“ aus. Die Wahrscheinlichkeit eines Ereignisses hängt nicht von vergangenen Versuchen ab. Daher bleibt die Ereignisrate konstant.
„Erinnerungslosigkeit“ bedeutet, dass die verbleibende Lebensdauer einer Komponente unabhängig von ihrem gegenwärtigen Alter ist. Die Eigenschaft der Erinnerungslosigkeit wird z. B. durch zufällige Versuche eines Münzwurfs demonstriert. Im Gegensatz dazu ist ein System, das dem Verschleiß unterliegt und daher mit steigender Lebensdauer eine höhere Ausfallwahrscheinlichkeit hat, nicht „erinnerungslos“.
