Betaverteilung

Verwenden Sie die Betaverteilung für Zufallsvariablen zwischen 0 und 1. Die Betaverteilung wird häufig zum Modellieren von Verteilungen von Ordnungsstatistiken – z. B. weist die Statistik der k-ten Ordnung einer Stichprobe von n gleichverteilten Variablen (0; 1) eine Betaverteilung (k; n + 1 – k) auf – sowie zum Modellieren von Ereignissen verwendet, die durch minimale und maximale Werte definiert sind. Die Betaverteilung wird häufig neu skaliert, um die Zeit bis zum Abschluss einer Aufgabe zu modellieren. Die Betaverteilung wird auch in Bayes-Statistiken verwendet, z. B. als die A-priori-Verteilung einer Binomialwahrscheinlichkeit.

Die Betaverteilung ist eine stetige Verteilung, die durch zwei Formparameter definiert wird. Die Verteilung kann je nach den Werten der beiden Parameter unterschiedliche Formen annehmen.

Beide Formen sind gleich 1

Wenn beide Formen gleich 1 sind, entspricht die Betaverteilung der Gleichverteilung.

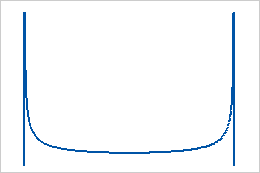
Beide Formen sind kleiner als 1

Wenn beide Formen kleiner als 1 sind, liegt eine U-förmige Verteilung vor.

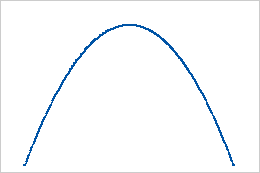
Beide Formen sind gleich und größer als 1

Wenn beide Formen gleich und größer als 1 sind, liegt eine symmetrische Verteilung vor.

Die erste Form ist größer als die zweite Form

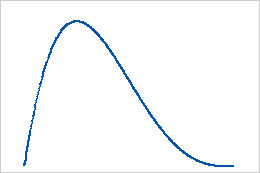
Wenn die erste Form größer als die zweite Form ist, weist die Verteilung eine nach links gerichtete Schiefe auf.

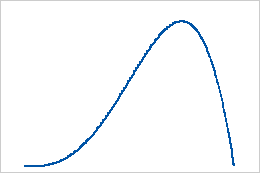
Die erste Form ist kleiner als die zweite Form

Wenn die erste Form kleiner als die zweite Form ist, weist die Verteilung eine nach rechts gerichtete Schiefe auf.