Sie können für eine im Menü ausgewählte Verteilung Werte für Dichtefunktionen, kumulative Verteilungsfunktionen oder inverse kumulative Wahrscheinlichkeiten der Daten berechnen.
- Dichtefunktion (PDF)
- Die Kurve der Dichtefunktion (PDF) zeigt Bereiche mit höherer und geringerer Wahrscheinlichkeit für die Werte der Zufallsvariablen. Bei einer Normalverteilung entspricht der höchste PDF-Wert beispielsweise dem Mittelwert, während sich die niedrigeren PDF-Werte in den Randbereichen der Verteilung befinden.
- Kumulative Verteilungsfunktion (CDF)
- Die kumulative Verteilungsfunktion (CDF) berechnet die kumulative Wahrscheinlichkeit für einen angegebenen Variablenwert. Mit der CDF können Sie die Wahrscheinlichkeit ermitteln, mit der eine zufällig aus der Grundgesamtheit entnommene Beobachtung kleiner oder gleich einem bestimmten Wert ist. Eine kumulative Verteilungsfunktion kann beispielsweise den Anteil von Bäumen in einem Wald veranschaulichen, die einen Durchmesser von 10 Zoll oder weniger aufweisen.
- Inverse kumulative Verteilungsfunktion (ICDF)
- Die inverse kumulative Verteilungsfunktion (ICDF) gibt den Wert der Variablen an, der einer bestimmten kumulativen Wahrscheinlichkeit zugeordnet ist. Ein Zuverlässigkeitstechniker möchte beispielsweise die Zeiten ermitteln, nach denen bestimmte Anteile von Bauteilen ausgefallen sind. Er kann die ICDF verwenden, um das 95. Perzentil der Verteilung der Ausfallzeiten zu bestimmen.
Beispiele für stetige Verteilungen
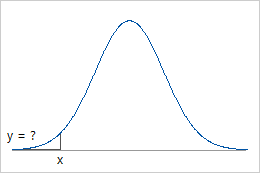
Verwenden Sie die PDF, wenn Sie x kennen und den entsprechenden y-Wert auf der Kurve ermitteln möchten.
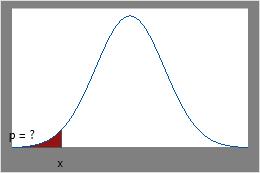
CDF
Verwenden Sie die CDF, wenn Sie x kennen und die Fläche unter der Kurve ermitteln möchten.
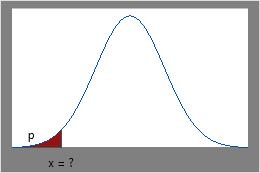
ICDF
Verwenden Sie die ICDF, wenn Sie die kumulative Fläche unter der Kurve kennen und den x-Wert ermitteln möchten.
