Was ist die Dichtefunktion (PDF)?
Mit der Dichtefunktion lassen sich Bereiche mit höherer und geringerer Wahrscheinlichkeit für die Werte einer Zufallsvariablen identifizieren.
Beispiel einer diskreten PDF
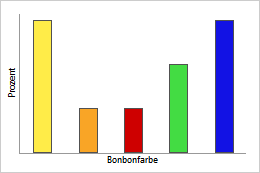
Diskrete PDF
In diesem Balkendiagramm wird die PDF für jede Bonbonfarbe angezeigt. Jeder Balken stellt die Wahrscheinlichkeit von Bonbons der betreffenden Farbe dar, die als Prozentsatz ausgedrückt wird.
Beispiel einer stetigen PDF
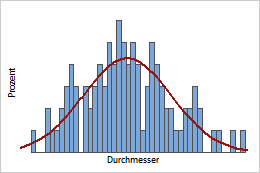
Stetige PDF
Die Kurve ist die PDF für den Korkendurchmesser. Verwenden Sie die PDF, um Bereiche mit höherer und geringerer Wahrscheinlichkeit für die Werte einer Zufallsvariablen identifizieren. So hat beispielsweise nur ein kleiner Prozentsatz von Korken (1 %) einen kleineren Durchmesser als 2,8 cm.
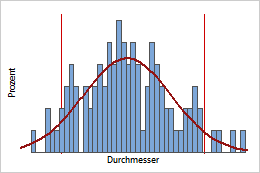
Stetige PDF mit Spezifikationsgrenzen
Wenn die Spezifikationsgrenzen für den Korkendurchmesser 2,85 cm bis 3,15 cm sind, kann die PDF die Wahrscheinlichkeitsdichte aller Korken aus diesem Prozess angeben, die die Spezifikationen erfüllen.
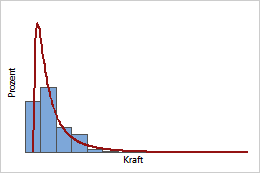
Lognormale PDF
Da beim Entkorken von Weinflaschen gelegentlich eine ungewöhnlich große Kraft aufgewendet werden muss, folgen Messwerte dieser Kraft häufig einer Verteilung mit einem langen rechten Randbereich, z. B. der lognormalen Verteilung.
