Beispiel für das Verwenden der ICDF zum Festlegen von Garantiezeiträumen
Zum Beispiel untersucht ein Gerätehersteller die Ausfallzeiten für das Heizelement in seinen Toastern. Sie wollen bestimmen, wann bestimmte Anteile der Heizelemente ausfallen, um die Garantiedauer festzulegen. Die Ausfallzeiten der Heizelemente folgen einer Normalverteilung mit einem Mittelwert von 1000 Stunden und einer Standardabweichung von 300 Stunden. Die Wahrscheinlichkeitsdichtefunktion (PDF) hilft, Bereiche mit höherer und niedriger Ausfallwahrscheinlichkeit zu identifizieren. Die inverse CDF gibt für jede kumulative Wahrscheinlichkeit die entsprechende Ausfallzeit an.
Verwenden Sie die inverse CDF, um die Zeit zu schätzen, zu der 5 % der Heizelemente ausfallen, Zeiten, in denen 95 % aller Heizelemente ausfallen, oder zu der Zeit, in der nur noch 5 % der Heizelemente übrig sind. Die inverse CDF für spezifische kumulative Wahrscheinlichkeiten entspricht der Ausfallzeit auf der rechten Seite des schattierten Bereichs unter der PDF-Kurve.
Bestimmen Sie den Zeitpunkt, zu dem 5 % durchfallen
- Wählen Sie .
- Wählen Sie Inverse kumulative Wahrscheinlichkeit aus. Geben Sie im Feld Mittelwert den Wert 1000 ein. Geben Sie im Feld Standardabweichung den Wert 300 ein. Geben Sie im Feld Eingabekonstante den Wert 0,05 ein.
- Klicken Sie auf OK.
Der Zeitpunkt, zu dem voraussichtlich 5 % der Heizelemente ausgefallen sind, ist der inverse CDF von 0,05 oder 506,544 Stunden.
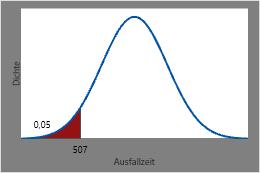
Dieses Diagramm veranschaulicht die umgekehrte CDF.
Bestimme Zeiten, zwischen denen 95 % scheitern
- Wählen Sie .
- Wählen Sie Inverse kumulative Wahrscheinlichkeit aus. Geben Sie im Feld Mittelwert den Wert 1000 ein. Geben Sie im Feld Standardabweichung den Wert 300 ein. Geben Sie im Feld Eingabekonstante den Wert 0,025 ein. Klicken Sie auf OK.
Der Zeitpunkt, zu dem voraussichtlich 2,5 % der Heizelemente ausgefallen sind, ist der inverse CDF von 0,025 oder 412 Stunden.
- Wiederhole Schritt 2, gib aber 0,975 statt 0,025ein. Klicken Sie auf OK.Der Zeitpunkt, zu dem voraussichtlich 97,5 % der Heizelemente ausgefallen sind, ist der inverse CDF von 0,975 oder 1588 Stunden.
Daher sind die Zeiten, zwischen denen 95 % aller Heizelemente voraussichtlich ausfallen, der inverse CDF von 0,025 und der inverse CDF von 0,975 bzw. 412 Stunden und 1588 Stunden.
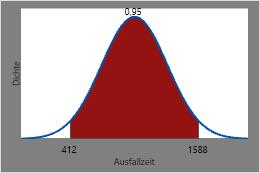
Dieses Diagramm veranschaulicht die umgekehrte CDF.
Bestimmen des Zeitpunkts, zu dem nur noch 5 % verbleiben
- Wählen Sie .
- Wählen Sie Inverse kumulative Wahrscheinlichkeit aus. Geben Sie im Feld Mittelwert den Wert 1000 ein. Geben Sie im Feld Standardabweichung den Wert 300 ein. Geben Sie im Feld Eingabekonstante den Wert 0,95 ein.
- Klicken Sie auf OK.
Der Zeitpunkt, zu dem nur 5 % der Heizelemente voraussichtlich verbleiben werden, ist die umgekehrte CDF von 0,95 oder 1493 Stunden.
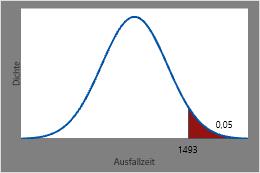
Dieses Diagramm veranschaulicht die umgekehrte CDF.
Beispiel für die Verwendung der CDF und der ICDF mit der hypergeometrischen Verteilung
Wenn man versucht, die inverse kumulative Wahrscheinlichkeit einer diskreten Verteilung zu bestimmen, enthält die Ausgabe in zwei Spaltensätze.
Angenommen, Sie haben die inverse kumulative Wahrscheinlichkeit eines Verhältniss, p. Die erste Spaltenmenge in der Ausgabe listet das größte x auf, so dass P(X ≤ x) ≤ p ist. Die zweite Spaltenmenge listet das kleinste x auf, so dass P(X ≤ x) ≥ p ist.
Berechnen der kumulativen Wahrscheinlichkeit einer hypergeometrischen Verteilung
- Im Arbeitsblatt Spalte C1 geben Sie 0 1 2ein.
C1 0 1 2 - Wählen Sie .
- Wählen Sie Kumulative Wahrscheinlichkeit aus.
- In Größe der Grundgesamtheit (N), Typ 20000.
- In Ereigniszahl in Grundgesamtheit (M), Typ 2000.
- In Stichprobenumfang (n), Typ 20.
- Wähle Eingabespalte und gib C1ein. Klicken Sie auf OK.
Kumulative Verteilungsfunktion
- P(X ≤ 0) = 0,121448. Die Wahrscheinlichkeit, dass 0 Fehler auftreten, liegt bei etwa 12 %.
- P(X ≤ 1) = 0,391619. Die Wahrscheinlichkeit, dass 0 oder 1 Fehler auftreten, liegt bei etwa 39 %.
- P(X ≤ 2) = 0,676941. Die Wahrscheinlichkeit, dass 0, 1 oder 2 Fehler auftreten, liegt bei etwa 68 %.
Berechnen Sie die inverse kumulative Wahrscheinlichkeit einer hypergeometrischen Verteilung
Da Sie nun die kumulativen Wahrscheinlichkeiten kennen, die mit der Anzahl der Defekte verbunden sind, berechnen Sie die inverse kumulative Wahrscheinlichkeit.
Angenommen, Sie möchten die Anzahl der Defekte x berechnen, so dass die kumulative Wahrscheinlichkeit p 0,50 beträgt. Aus den vorherigen Ergebnissen wissen Sie, dass P(X ≤ 1 ) = 0,391619 und P(X ≤ 2) = 0,676941 gilt. Da die hypergeometrische Verteilung eine diskrete Verteilung ist, kann die Anzahl der Defekte nicht zwischen 1 und 2 liegen. Mit anderen Worten, du hast vielleicht 1 oder 2 Defekte, aber nicht 1,4 Defekte. Wenn Sie also 0,50auswählen Eingabekonstante und eingeben, berechnet Minitab beide Wahrscheinlichkeiten im Output, wie im folgenden Beispiel gezeigt:
- Wählen Sie .
- Wählen Sie Inverse kumulative Wahrscheinlichkeit aus.
- In Größe der Grundgesamtheit (N), Typ 20000.
- In Ereigniszahl in Grundgesamtheit (M), Typ 2000.
- In Stichprobenumfang (n), Typ 20.
- Wähle Eingabekonstante, und tippe 0,50ein. Klicken Sie auf OK.
Inverse kumulative Verteilungsfunktion
Die erste Wahrscheinlichkeit gibt einen Wert von x an, bei dem P(X ≤ x) < p, und die zweite Wahrscheinlichkeit den kleinsten Wert von x, bei dem P(X ≤ x) ≥ p. In diesem Beispiel entspricht die erste Wahrscheinlichkeit der größten Anzahl von Ausfällen, x = 2, bei der P(X ≤ 2) < 0,5, und die 2<1 id="127">.</1> Ausfällen, x = 3, bei der P(X ≤ 3) ≥ 0,5.
Verwenden der ICDF zum Berechnen von kritischen Werten
Mit Minitab können Sie einen kritischen Wert für einen Hypothesentest berechnen, statt diesen in einer Tabelle nachzuschlagen.
Angenommen, Sie führen einen Chi-Quadrat-Test mit einem α = 0,02 und 12 Freiheitsgraden durch. Welchem kritischen Wert entspricht dies? Der Wert α = 0,02 entspricht einer kumulativen Wahrscheinlichkeit von 1 – 0,02 = 0,98.
- Wählen Sie .
- Wählen Sie Inverse kumulative Wahrscheinlichkeit aus.
- Geben Sie im Feld Freiheitsgrade den Wert 12 ein.
- Wähle Eingabekonstante und gib 0,98ein.
- Klicken Sie auf OK.
Minitab zeigt den kritischen Wert 24,054 an. Beim Chi-Quadrat-Test kann man, wenn die Teststatistik größer als der kritische Wert ist, schließen, dass es statistische Hinweise gibt, die die Nullhypothese ablehnen.
Hinweis
Dieses Beispiel verwendet die Chi-Quadrat-Verteilung. Allerdings befolgen Sie dieselben Schritte für jede Distribution, die Sie auswählen.
