Beispiel für die Verwendung der CDF zur Berechnung von Füllgewichten
Zum Beispiel folgen Limonadenfüllungsgewichte einer Normalverteilung mit einem Mittelwert von 12 Unzen und einer Standardabweichung von 0,25 Unzen. Die Wahrscheinlichkeitsdichtefunktion (PDF) beschreibt die Wahrscheinlichkeit möglicher Werte des Füllgewichts. Die CDF liefert die kumulative Wahrscheinlichkeit für jeden x-Wert.
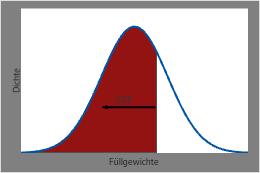
Die CDF für Füllgewichte an einem bestimmten Punkt entspricht dem schattierten Bereich unter der PDF-Kurve links von diesem Punkt.
Verwenden Sie die CDF, um die Wahrscheinlichkeit zu bestimmen, dass eine zufällig ausgewählte Dose Limonade ein Füllgewicht von weniger als 11,5 Unzen, mehr als 12,5 Unzen oder zwischen 11,5 und 12,5 Unzen hat.
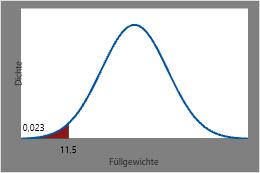
Die Wahrscheinlichkeit, dass eine zufällig ausgewählte Limonadendodose ein Füllgewicht von weniger als oder gleich 11,5 Unzen hat, beträgt die CDF bei 11,5 oder etwa 0,023.
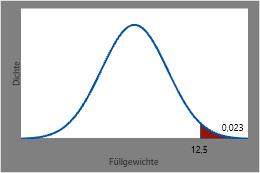
Die Wahrscheinlichkeit, dass eine zufällig ausgewählte Dose Limonade ein Füllgewicht von mehr als 12,5 Unzen hat, beträgt 1 minus die CDF bei 12,5 (0,977), also ungefähr 0,023.
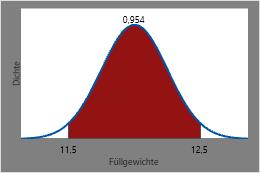
Die Wahrscheinlichkeit, dass eine zufällig ausgewählte Dose Limonade ein Füllgewicht zwischen 11,5 und 12,5 Unzen hat, beträgt die CDF bei 12,5 minus die CDF bei 11,5 oder etwa 0,954.
Verwenden der CDF zum Berechnen von p-Werten
Um einen p-Wert für einen F-Test zu berechnen, muss man zunächst die kumulative Verteilungsfunktion (CDF) berechnen. Der p-Wert beträgt 1 – CDF.
Angenommen, Sie führen eine multiple lineare Regressionsanalyse mit folgenden Freiheitsgraden durch: DF (Regression) = 3; DF (Fehler) = 25; und F-- Statistik = 2,44.
Berechnen eines p-Werts für den F-Test
- Wählen Sie .
- Wählen Sie Kumulative Wahrscheinlichkeit aus.
- Geben Sie im Feld Nichtzentralitätsparameter den Wert 0 ein.
- Geben Sie im Feld Freiheitsgrade des Zählers den Wert 3 ein.
- Geben Sie im Feld Freiheitsgrade des Nenners den Wert 25 ein.
- Wählen Eingabekonstante Sie und geben Sie 2.44ein.
- Geben Sie im Feld Optional speichern die Spalte K1 ein. Klicken Sie auf OK. K1 enthält die kumulative Verteilungsfunktion.
Subtrahieren des p-Werts von 1 mit dem Rechner
- Wählen Sie aus.
- In Ergebnis speichern in Variable, geben Sie den P-Wertein.
- Geben Sie im Feld Ausdruck die Spalte 1-K1 ein. Klicken Sie auf OK.
Hinweis
Dieses Beispiel bezieht sich auf eine F-Verteilung; Sie können jedoch eine ähnliche Methode für andere Verteilungen verwenden.
