Was ist eine stetige Verteilung?
Eine stetige Verteilung beschreibt die Wahrscheinlichkeiten für die möglichen Werte einer stetigen Zufallsvariablen. Als stetige Zufallsvariable wird eine Zufallsvariable mit einer Menge möglicher Werte (der Spannweite) bezeichnet, die unendlich und nicht zählbar ist.
Die Wahrscheinlichkeit einer stetigen Zufallsvariablen (x) ist als die Fläche unter der Kurve ihrer PDF definiert. Daher können nur Wertebereiche eine Wahrscheinlichkeit ungleich null aufweisen. Die Wahrscheinlichkeit, mit der eine stetige Zufallsvariable gleich einem bestimmten Wert ist, liegt stets bei null.
Beispiel für die Verteilung von Gewichten
Die stetige Normalverteilung kann die Verteilung des Gewichts erwachsener Männer beschreiben. Sie können z. B. die Wahrscheinlichkeit berechnen, mit der ein Mann zwischen 160 und 170 Pfund wiegt.
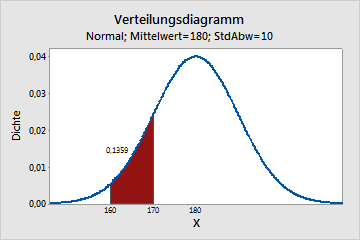
Verteilungsdiagramm des Gewichts erwachsener Männer
Der eingefärbte Bereich unter der Kurve in diesem Beispiel stellt den Bereich zwischen 160 und 170 Pfund dar. Die Fläche dieses Bereichs beträgt 0,136; daher liegt die Wahrscheinlichkeit, mit der ein zufällig ausgewählter Mann zwischen 160 und 170 Pfund wiegt, bei 13,6 %. Die gesamte Fläche unter der Kurve ist gleich 1,0.
Die Wahrscheinlichkeit, mit der x genau gleich einem bestimmten Wert ist, liegt jedoch stets bei null, da die Fläche unter der Kurve bei einem beliebigen einzelnen Punkt, der keine Breite besitzt, null ist. Zum Beispiel liegt die Wahrscheinlichkeit, mit der ein Mann mit unendlicher Präzision genau 190 Pfund wiegt, bei null. Sie können eine Wahrscheinlichkeit ungleich null berechnen, mit der ein Mann mehr als 190 Pfund, weniger als 190 Pfund oder zwischen 189,9 und 190,1 Pfund wiegt, doch die Wahrscheinlichkeit, mit der er exakt 190 Pfund wiegt, ist null.
Was ist eine diskrete Verteilung?
Eine diskrete Verteilung beschreibt die Wahrscheinlichkeit, mit der jeder einzelne Wert einer diskreten Zufallsvariablen auftritt. Eine diskrete Zufallsvariable ist eine Zufallsvariable mit zählbaren Werten, z. B. eine Liste nicht negativer ganzer Zahlen.
Mit einer diskreten Wahrscheinlichkeitsverteilung kann jedem möglichen Wert der diskreten Zufallsvariablen eine Wahrscheinlichkeit ungleich null zugeordnet werden. Daher wird eine diskrete Wahrscheinlichkeitsverteilung oft in tabellarischer Form dargestellt.
Beispiel: Anzahl der Kundenbeschwerden
| x | P (X = x) |
|---|---|
| 5 | 0,037833 |
| 10 | 0,12511 |
| 15 | 0,034718 |
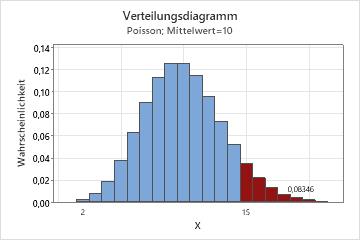
Verteilungsdiagramm der Anzahl der Kundenbeschwerden
Die eingefärbten Balken in diesem Beispiel stellen die Häufigkeiten dar, wenn die Anzahl der Kundenbeschwerden an einem Tag 15 oder mehr beträgt. Die Höhe der Balken summiert sich auf 0,08346; die Wahrscheinlichkeit, dass die Anzahl der Anrufe pro Tag 15 oder mehr beträgt, liegt also bei 8,35 %.
