Ein Gesundheitsberater möchte die Bewertungen der Zufriedenheit von Patienten für zwei Krankenhäuser vergleichen. Der Berater führt einen Randomisierungstest für den Mittelwert bei zwei Stichproben durch, um zu ermitteln, ob sich die Patientenbewertungen für die Krankenhäuser unterscheiden.
- Öffnen Sie die Beispieldaten Krankenhausvergleich.MWX.
- Wählen Sie aus.
- Geben Sie im Feld Stichproben die Spalte Bewertung ein.
- Geben Sie im Feld Stichproben-IDs die Spalte Krankenhaus ein.
- Klicken Sie auf Optionen. Geben Sie den Wert 1 im Feld Basis für Zufallszahlengenerator ein.
Hinweis
Durch die Verwendung von Basis für Zufallszahlengenerator wird sichergestellt, dass die Ergebnisse dem Beispiel entsprechen.
- Klicken Sie in den einzelnen Dialogfeldern auf OK.
Interpretieren der Ergebnisse
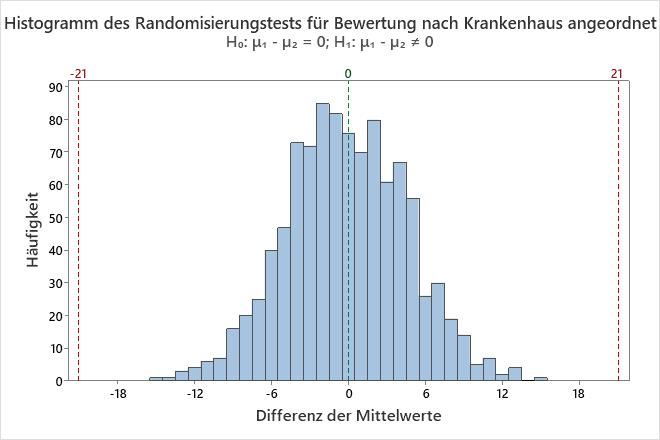
Die Nullhypothese besagt, dass die Differenz zwischen den Patientenbewertungen der Krankenhäuser 0 ist. Da der p-Wert kleiner als 0,002 und somit kleiner als das Signifikanzniveau 0,05 ist, weist der Berater die Nullhypothese zurück und folgert, dass die Differenz zwischen den Patientenbewertungen der Krankenhäuser ungleich 0 ist. Das Histogramm zeigt, dass die Bootstrap-Verteilung anscheinend normalverteilt ist, so dass der Berater den Ergebnissen vertrauen kann.
Die Differenz zwischen den beobachteten Mittelwerten beträgt 21, was darauf hinweist, dass die Bewertungen der Patientenzufriedenheit für Krankenhaus A höher als für Krankenhaus B sind.
Methode
| μ₁: Mittelwert der Grundgesamtheit von Bewertung, wenn Krankenhaus = A |
|---|
| µ₂: Mittelwert der Grundgesamtheit von Bewertung, wenn Krankenhaus = B |
| Differenz: μ₁ - µ₂ |
Beobachtete Stichproben
| Krankenhaus | N | Mittelwert | StdAbw | Varianz | Minimum | Median | Maximum |
|---|---|---|---|---|---|---|---|
| A | 20 | 80,30 | 8,18 | 66,96 | 62,00 | 79,00 | 98,00 |
| B | 20 | 59,30 | 12,43 | 154,54 | 35,00 | 58,50 | 89,00 |
Differenz der beobachteten Mittelwerte
| Mittelwert von A – Mittelwert von B = 21,000 |
|---|
Randomisierungstest
| Nullhypothese | H₀: μ₁ - µ₂ = 0 |
|---|---|
| Alternativhypothese | H₁: μ₁ - µ₂ ≠ 0 |
| Anzahl von Stichprobenwiederholungen | Durchschnitt | StdAbw | p-Wert |
|---|---|---|---|
| 1000 | -0,185 | 4,728 | < 0,002 |
