Führen Sie die folgenden Schritte aus, um einen Randomisierungstest für den Mittelwert bei einer Stichprobe zu interpretieren. Zu den wichtigsten Ausgaben zählen das Histogramm und der p-Wert.
Schritt 1: Untersuchen der Form Ihrer Bootstrap-Verteilung
Verwenden Sie ein Histogramm, um die Form Ihrer Bootstrap-Verteilung zu untersuchen. Die Bootstrap-Verteilung ist die Verteilung der Mittelwerte aus jeder Stichprobenwiederholung. Die Bootstrap-Verteilung sollte normalverteilt erscheinen. Wenn die Bootstrap-Verteilung nicht normalverteilt ist, sind die Ergebnisse nicht vertrauenswürdig.
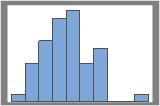
50 Stichprobenwiederholungen
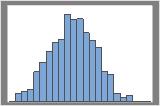
1000 Stichprobenwiederholungen
Die Verteilung lässt sich im Allgemeinen leichter mit einer höheren Anzahl von Stichprobenwiederholungen bestimmen. In diesen Daten ist die Verteilung für 50 Stichprobenwiederholungen beispielsweise mehrdeutig. Bei 1000 Stichprobenwiederholungen sieht die Form annähernd normalverteilt aus.
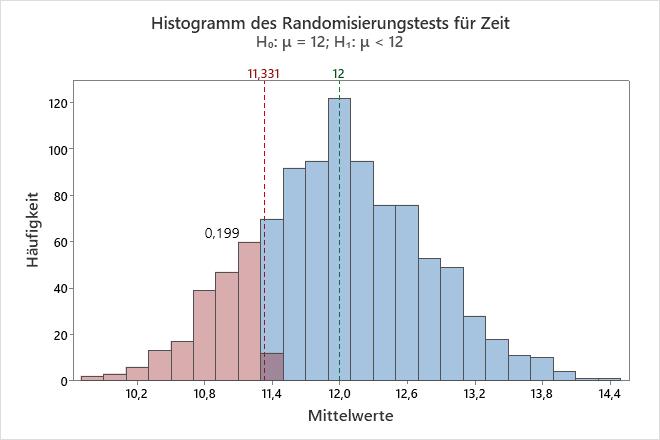
In diesem Histogramm ist die Bootstrap-Verteilung anscheinend normalverteilt.
Schritt 2: Bestimmen, ob die Testergebnisse statistisch signifikant sind
Um zu ermitteln, ob die Differenz zwischen dem Mittelwert der Grundgesamtheit und dem hypothetischen Mittelwert statistisch signifikant ist, vergleichen Sie den p-Wert mit dem Signifikanzniveau. In der Regel ist ein Signifikanzniveau (als α oder Alpha bezeichnet) von 0,05 gut geeignet. Ein Signifikanzniveau von 0,05 gibt ein Risiko von 5 % an, dass auf eine vorhandene Differenz geschlossen wird, während tatsächlich keine vorhanden ist.
p-Wert ≤ α: Die Differenz zwischen den Mittelwerten ist statistisch signifikant (H0 verwerfen)
Wenn der p-Wert kleiner oder gleich dem Signifikanzniveau ist, weisen Sie die Nullhypothese zurück. Sie können schlussfolgern, dass die Differenz zwischen dem Mittelwert der Grundgesamtheit und dem Hypothesenmittelwert statistisch signifikant ist. Verwenden Sie Bootstrapping
für Funktion, 1 Stichprobe, um ein Konfidenzintervall zu berechnen und zu bestimmen, ob die Differenz praktisch signifikant ist. Weitere Informationen finden Sie unter Statistische und praktische Signifikanz.
p-Wert > α: Die Differenz zwischen den Mittelwerten ist statistisch nicht signifikant (H0 nicht verwerfen)
Wenn der p-Wert größer als das Signifikanzniveau ist, weisen Sie die Nullhypothese nicht zurück. Es liegen nicht genügend Anzeichen für die Schlussfolgerung vor, dass die Differenz zwischen dem Mittelwert der Grundgesamtheit und dem hypothetischen Mittelwert statistisch signifikant ist.
Beobachtete Stichprobe
Variable
N
Mittelwert
StdAbw
Varianz
Summe
Minimum
Median
Maximum
Zeit
16
11,331
3,115
9,702
181,300
7,700
10,050
16,000
Randomisierungstest
Nullhypothese
H₀: μ = 12
Alternativhypothese
H₁: μ < 12
Anzahl von Stichprobenwiederholungen
Mittelwert
StdAbw
p-Wert
1000
11,9783
0,7625
0,199
Wichtigste Ergebnisse: p-Wert
In diesen Ergebnissen besagt die Alternativhypothese, dass die mittlere Reaktionszeit kürzer als 12 Minuten ist. Da der p-Wert 0,203 beträgt und somit höher als das Signifikanzniveau von 0,05 ist, weisen Sie die Nullhypothese nicht zurück. Sie können nicht schlussfolgern, dass die mittlere Reaktionszeit kürzer als 12 Minuten ist.
