In diesem Thema
Histogramm
In einem Histogramm werden die Stichprobenwerte in eine Reihe von Intervallen unterteilt, und die Häufigkeit der Datenwerte in jedem Intervall wird in Form eines Balkens abgebildet.
Interpretation
50 Stichprobenwiederholungen
1000 Stichprobenwiederholungen
Die Verteilung lässt sich im Allgemeinen leichter mit einer höheren Anzahl von Stichprobenwiederholungen bestimmen. In diesen Daten ist die Verteilung für 50 Stichprobenwiederholungen beispielsweise mehrdeutig. Bei 1000 Stichprobenwiederholungen sieht die Form annähernd normalverteilt aus.
Im Histogramm werden die Ergebnisse des Hypothesentests visuell dargestellt. Minitab korrigiert die Daten so, dass das Zentrum der Stichprobenwiederholungen identisch mit dem Hypothesenmittelwert ist. Bei einem einseitigen Test wird eine Referenzlinie am Mittelwert der ursprünglichen Stichprobe gezeichnet. Bei einem zweiseitigen Test wird eine Referenzlinie am Mittelwert der ursprünglichen Stichprobe und in derselben Distanz auf der gegenüberliegenden Seite des Hypothesenmittelwerts gezeichnet. der p-Wert ist der Anteil der Stichprobenmittelwerte, die extremer als die Werte an den Referenzlinien sind. Mit anderen Worten: Der p-Wert ist der Anteil der Stichprobenmittelwerte, die genau so extrem wie die ursprüngliche Stichprobe sind, wenn angenommen wird, dass die Nullhypothese wahr ist. Diese Mittelwerte sind im Histogramm rot gefärbt.
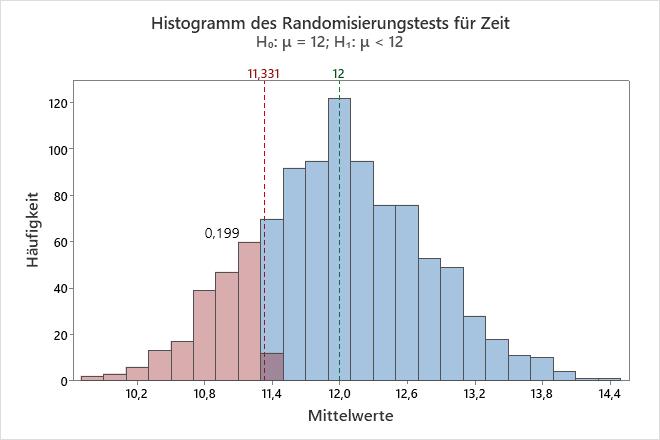
In diesem Histogramm ist die Bootstrap-Verteilung anscheinend normalverteilt. Der p-Wert 0,2030 zeigt, dass 20,3 % der Stichprobenmittelwerte kleiner als der Mittelwert der ursprünglichen Stichprobe sind.
Einzelwertdiagramm
In einem Einzelwertdiagramm werden die Einzelwerte in der Stichprobe gezeigt. Jeder Kreis stellt eine Beobachtung dar. Ein Einzelwertdiagramm ist besonders hilfreich, wenn nur eine kleine Anzahl von Beobachtungen vorliegt und Sie zudem die Auswirkung jeder Beobachtung bewerten müssen.
Hinweis
Minitab zeigt nur dann ein Einzelwertdiagramm an, wenn Sie nur eine Stichprobenwiederholung ziehen. Minitab zeigt sowohl die ursprünglichen Daten als auch die Daten aus der Stichprobenwiederholung an.
Interpretation
Minitab korrigiert die Daten so, dass das Zentrum der Stichprobenwiederholungen identisch mit dem Hypothesenmittelwert ist. Zunächst berechnet Minitab die Differenz zwischen dem Hypothesenmittelwert und dem Mittelwert der ursprünglichen Stichprobe. Anschließend wird die Differenz von Minitab zu jedem Wert in der ursprünglichen Stichprobe addiert bzw. von jedem Wert in der ursprünglichen Stichprobe subtrahiert. Die Stichprobenwiederholungen werden aus diesen korrigierten Daten gezogen.
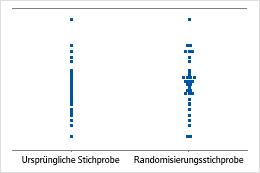
Stichprobenmittelwert ist gleich dem Hypothesenmittelwert
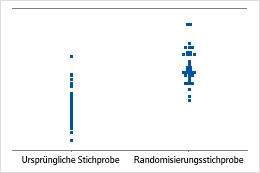
Stichprobenmittelwert ist 2 Standardabweichungen kleiner als der Hypothesenmittelwert
Nullhypothese und Alternativhypothese
- Nullhypothese
- Die Nullhypothese besagt, dass ein Parameter einer Grundgesamtheit (z. B. der Mittelwert, die Standardabweichung usw.) gleich einem Hypothesenwert ist. Die Nullhypothese ist oft eine anfängliche Behauptung auf der Grundlage von früheren Analysen oder Fachwissen.
- Alternativhypothese
- Die Alternativhypothese besagt, dass ein Parameter einer Grundgesamtheit kleiner, größer oder abweichend vom Hypothesenwert in der Nullhypothese ist. Die Alternativhypothese ist die Hypothese, die Sie als wahr annehmen oder deren Wahrheit Sie nachweisen möchten.
Interpretation
In der Ausgabe können Sie mit Hilfe der Nullhypothese und der Alternativhypothese überprüfen, ob Sie den korrekten Wert für den hypothetischen Mittelwert eingegeben haben.
Beobachtete Stichprobe
| Variable | N | Mittelwert | StdAbw | Varianz | Summe | Minimum | Median | Maximum |
|---|---|---|---|---|---|---|---|---|
| Zeit | 16 | 11,331 | 3,115 | 9,702 | 181,300 | 7,700 | 10,050 | 16,000 |
Randomisierungstest
| Nullhypothese | H₀: μ = 12 |
|---|---|
| Alternativhypothese | H₁: μ < 12 |
| Anzahl von Stichprobenwiederholungen | Mittelwert | StdAbw | p-Wert |
|---|---|---|---|
| 1000 | 11,9783 | 0,7625 | 0,199 |
In diesen Ergebnissen besagt die Nullhypothese, dass der Mittelwert der Grundgesamtheit gleich 12 ist. Die Alternativhypothese besagt, dass der Mittelwert kleiner als 12 ist.
Anzahl von Stichprobenwiederholungen
Die Anzahl der Stichprobenwiederholungen gibt die Häufigkeit an, mit der Minitab eine Zufallsstichprobe mit Zurücklegen aus dem ursprünglichen Datensatz zieht. Im Allgemeinen empfiehlt sich eine große Anzahl von Stichprobenwiederholungen.
Minitab korrigiert die Daten so, dass das Zentrum der Stichprobenwiederholungen identisch mit dem Hypothesenmittelwert ist. Zunächst berechnet Minitab die Differenz zwischen dem Hypothesenmittelwert und dem Mittelwert der ursprünglichen Stichprobe. Anschließend wird die Differenz von Minitab zu jedem Wert in der ursprünglichen Stichprobe addiert bzw. von jedem Wert in der ursprünglichen Stichprobe subtrahiert. Die Stichprobenwiederholungen werden aus diesen korrigierten Daten gezogen. Der Stichprobenumfang für jede Stichprobenwiederholung ist gleich dem Stichprobenumfang des ursprünglichen Datensatzes. Die Anzahl der Stichprobenwiederholungen ist gleich der Anzahl der Beobachtungen im Histogramm.
Mittelwert
Der Mittelwert ist die Summe aller Mittelwerte in der Bootstrap-Stichprobe, dividiert durch die Anzahl der Stichprobenwiederholungen. Minitab passt die Daten so an, dass das Zentrum der Stichprobenwiederholungen identisch mit dem Hypothesenmittelwert ist.
Interpretation
Minitab zeigt zwei unterschiedliche Mittelwerte an, den Mittelwert der beobachteten Stichprobe und den Mittelwert der Bootstrap-Verteilung. Der Mittelwert der beobachteten Stichprobe ist ein Schätzwert des Mittelwerts der Grundgesamtheit. Der Mittelwert der Bootstrap-Verteilung liegt im Allgemeinen nahe dem Hypothesenmittelwert. Je größer die Differenz zwischen diesen beiden Werten ist, desto mehr Anzeichen gegen das Zutreffen der Nullhypothese sind zu erwarten.
StdAbw (Bootstrap-Stichprobe)
Die Standardabweichung ist das am häufigsten verwendete Maß für die Streuung bzw. die Streubreite der Daten um den Mittelwert. Die Standardabweichung einer Grundgesamtheit wird häufig mit dem Zeichen σ (Sigma) angegeben, während mit s die Standardabweichung einer Stichprobe dargestellt wird. Eine zufällige oder natürliche Streuung eines Prozesses wird häufig auch als Rauschen bezeichnet. Da die Standardabweichung in der gleichen Einheit wie die Daten angegeben wird, lässt sie sich in der Regel einfacher als die Varianz interpretieren.
Die Standardabweichung der Bootstrap-Stichproben (auch als Bootstrap-Standardfehler bezeichnet) ist ein Schätzwert der Standardabweichung der Stichprobenverteilung des Mittelwerts. Da der Bootstrap-Standardfehler die Streuung der Stichprobenmittelwerte angibt, während die Standardabweichung der beobachteten Stichproben die Streuung einzelner Beobachtungen angibt, ist der Bootstrap-Standardfehler kleiner.
Interpretation
Verwenden Sie die Standardabweichung, um zu ermitteln, wie stark die Mittelwerte der Bootstrap-Stichprobe um den Gesamtmittelwert gestreut sind. Ein höherer Wert der Standardabweichung verweist auf eine größere Streubreite der Mittelwerte. Eine Faustregel für die Normalverteilung besagt, dass etwa 68 % der Werte innerhalb einer Standardabweichung vom Gesamtmittelwert, 95 % der Werte innerhalb zwei Standardabweichungen und 99,7 % der Werte innerhalb drei Standardabweichungen liegen.
Verwenden Sie die Standardabweichung der Bootstrap-Stichproben, um die Genauigkeit der Bootstrap-Mittelwerte zu schätzen. Ein kleinerer Wert verweist auf eine höhere Genauigkeit. Eine größere Standardabweichung in der ursprünglichen Stichprobe ergibt im Allgemeinen einen größeren Bootstrap-Standardfehler und einen weniger trennscharfen Hypothesentest. Auch ein kleinerer Stichprobenumfang führt in der Regel zu einem größeren Bootstrap-Standardfehler und einem weniger trennscharfen Hypothesentest.

Krankenhaus 1
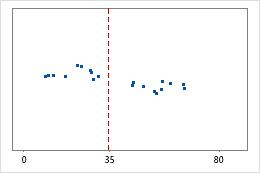
Krankenhaus 2
Zeit bis zur Entlassung in Krankenhäusern
Verwaltungsangestellte zeichnen die Zeit bis zur Entlassung von Patienten auf, die in der Notaufnahme zweier Krankenhäuser behandelt werden. Obwohl die durchschnittliche Zeit bis zur Entlassung in etwa identisch ist (35 Minuten), weichen die Standardabweichungen deutlich voneinander ab. Die Standardabweichung für Krankenhaus 1 beträgt etwa 6. Im Durchschnitt weicht die Zeit bis zur Entlassung eines Patienten um etwa 6 Minuten vom Mittelwert (gestrichelte Linie) ab. Die Standardabweichung für Krankenhaus 2 beträgt etwa 20. Im Durchschnitt weicht die Zeit bis zur Entlassung eines Patienten um ca. 20 Minuten vom Mittelwert (gestrichelte Linie) ab.
p-Wert
Der p-Wert ist der Anteil der Stichprobenmittelwerte, die genauso extrem wie die ursprüngliche Stichprobe sind, wenn angenommen wird, dass die Nullhypothese wahr ist. Ein kleinerer p-Wert liefert stärkere Anzeichen dafür, dass die Nullhypothese nicht zutrifft.
Interpretation
Verwenden Sie den p-Wert, um zu ermitteln, ob der Mittelwert der Grundgesamtheit statistisch vom Hypothesenmittelwert abweicht.
- p-Wert ≤ α: Die Differenz zwischen den Mittelwerten ist statistisch signifikant (H0 verwerfen)
- Wenn der p-Wert kleiner oder gleich dem Signifikanzniveau ist, weisen Sie die Nullhypothese zurück. Sie können schlussfolgern, dass die Differenz zwischen dem Mittelwert der Grundgesamtheit und dem Hypothesenmittelwert statistisch signifikant ist. Verwenden Sie Bootstrapping für Funktion, 1 Stichprobe, um ein Konfidenzintervall zu berechnen und zu bestimmen, ob die Differenz praktisch signifikant ist. Weitere Informationen finden Sie unter Statistische und praktische Signifikanz.
- p-Wert > α: Die Differenz zwischen den Mittelwerten ist statistisch nicht signifikant (H0 nicht verwerfen)
- Wenn der p-Wert größer als das Signifikanzniveau ist, weisen Sie die Nullhypothese nicht zurück. Es liegen nicht genügend Anzeichen für die Schlussfolgerung vor, dass die Differenz zwischen dem Mittelwert der Grundgesamtheit und dem hypothetischen Mittelwert statistisch signifikant ist.
