Interpretieren der wichtigsten Ergebnisse für Bootstrapping für Mittelwerte, 2 Stichproben

Führen Sie die folgenden Schritte aus, um eine Bootstrapping-Analyse für Mittelwerte bei zwei Stichproben zu interpretieren. Zu den wichtigsten Ausgaben zählen das Histogramm, der Durchschnitt und das Konfidenzintervall.

In diesem Thema

Schritt 1: Untersuchen der Form Ihrer Bootstrap-Verteilung
Schritt 2: Bestimmen eines Konfidenzintervalls für den Mittelwert der Grundgesamtheit

Schritt 1: Untersuchen der Form Ihrer Bootstrap-Verteilung

Verwenden Sie ein Histogramm, um die Form Ihrer Bootstrap-Verteilung zu untersuchen. Die Bootstrap-Verteilung ist die Verteilung der Differenz der Mittelwerte aus den einzelnen Stichprobenwiederholungen. Die Bootstrap-Verteilung sollte normalverteilt erscheinen. Wenn die Bootstrap-Verteilung nicht normalverteilt ist, sind die Ergebnisse nicht vertrauenswürdig.

Die Verteilung lässt sich im Allgemeinen leichter mit einer höheren Anzahl von Stichprobenwiederholungen bestimmen. In diesen Daten ist die Verteilung für 50 Stichprobenwiederholungen beispielsweise mehrdeutig. Bei 1000 Stichprobenwiederholungen sieht die Form annähernd normalverteilt aus.

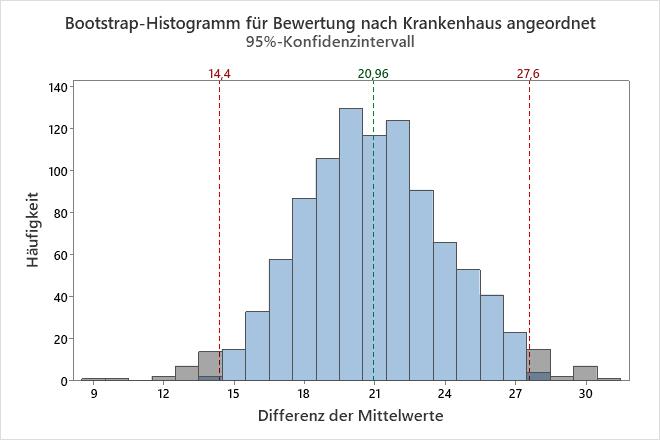
In diesem Histogramm ist die Bootstrap-Verteilung anscheinend normalverteilt.

Schritt 2: Bestimmen eines Konfidenzintervalls für den Mittelwert der Grundgesamtheit

Betrachten Sie zuerst die Differenz zwischen den Mittelwerten der Bootstrap-Stichprobe, und untersuchen Sie anschließend das Konfidenzintervall.

Die Differenz zwischen den Mittelwerten der Bootstrap-Stichprobe ist ein Schätzwert der Differenz zwischen den Mittelwerten der Grundgesamtheiten. Da die Differenz der Bootstrap-Stichprobe auf Stichprobendaten und nicht auf der vollständigen Grundgesamtheit basiert, ist es unwahrscheinlich, dass die Differenz der Bootstrap-Stichprobe gleich der Differenz zwischen den Mittelwerten der Grundgesamtheiten ist. Verwenden Sie das Konfidenzintervall, um die Differenz zwischen den Mittelwerten der Grundgesamtheiten besser schätzen zu können.

Konfidenzintervalle basieren auf der Stichprobenverteilung einer Statistik. Wenn eine Statistik im Hinblick auf den Schätzwert für einen Parameter nicht verzerrt ist, ist ihre Stichprobenverteilung um den wahren Wert des Parameters zentriert. Eine Bootstrapping-Verteilung entspricht annähernd der Stichprobenverteilung der Statistik. Daher liefern die mittleren 95 % der Werte aus der Bootstrapping-Verteilung ein 95%-Konfidenzintervall für den Parameter. Anhand des Konfidenzintervalls können Sie die praktische Signifikanz Ihres Schätzwerts für den Parameter der Grundgesamtheit beurteilen. Bestimmen Sie anhand Ihrer Fachkenntnisse, ob das Konfidenzintervall Werte umfasst, die in der jeweiligen Situation von praktischer Signifikanz sind.

Hinweis

Minitab berechnet kein Konfidenzintervall, wenn die Anzahl der Stichprobenwiederholungen zu klein ist, um ein genaues Konfidenzintervall zu erhalten.

Beobachtete Stichproben

Krankenhaus	N	Mittelwert	StdAbw	Varianz	Minimum	Median	Maximum
A	20	80,30	8,18	66,96	62,00	79,00	98,00
B	20	59,30	12,43	154,54	35,00	58,50	89,00

Differenz der beobachteten Mittelwerte

Mittelwert von A – Mittelwert von B = 21

Bootstrap-Stichproben für Differenz der Mittelwerte

Anzahl von Stichprobenwiederholungen	Durchschnitt	StdAbw	95%-KI für Differenz
1000	20,960	3,279	(14,400; 27,600)

Wichtigste Ergebnisse: Durchschnitt, 95%-KI für Differenz

In diesen Ergebnissen beträgt der Schätzwert für die Differenz der Grundgesamtheit 20,96. Sie können sich zu 95 % sicher sein, dass die Differenz der Grundgesamtheit zwischen 14,4 und 27,6 liegt.