In diesem Thema
Mittelwert
Ein häufig verwendetes Maß für das Zentrum einer Gruppe von Zahlen. Der Mittelwert wird auch als Durchschnitt bezeichnet. Es handelt sich um die Summe aller Beobachtungen dividiert durch die Anzahl der (nicht fehlenden) Beobachtungen.
Formel
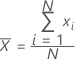
Notation
| Begriff | Beschreibung |
|---|---|
| xi | i-te Beobachtung |
| N | Anzahl der nicht fehlenden Beobachtungen |
Standardabweichung (StdAbw)
Die Standardabweichung der Stichprobe bietet ein Maß für die Streubreite der Daten. Sie entspricht der Quadratwurzel der Varianz der Stichprobe.
Formel
 , dann ist die Standardabweichung der Stichprobe:
, dann ist die Standardabweichung der Stichprobe:
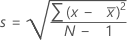
Notation
| Begriff | Beschreibung |
|---|---|
| x i | i-te Beobachtung |
 | Mittelwert der Beobachtungen |
| N | Anzahl der nicht fehlenden Beobachtungen |
Varianz
Die Varianz ist ein Maß der Streuung der Daten um ihren Mittelpunkt. Die Varianz ist gleich dem Quadrat der Standardabweichung.
Formel
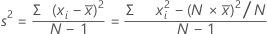
Notation
| Begriff | Beschreibung |
|---|---|
| xi | i-te Beobachtung |
 | Mittelwert der Beobachtungen |
| N | Anzahl der nicht fehlenden Beobachtungen |
Summe
Formel

Notation
| Begriff | Beschreibung |
|---|---|
| xi | i-te Beobachtung |
Minimum
Der kleinste Wert im Datensatz.
Median
Der Stichproben-Median liegt in der Mitte der Daten: Mindestens die Hälfte der Beobachtungen sind kleiner oder gleich und mindestens die Hälfte sind größer oder gleich dem Stichproben-Median.
Angenommen, eine Spalte enthält N Werte. Um den Median zu berechnen, ordnen Sie die Datenwerte zunächst vom kleinsten zum größten an. Wenn N eine ungerade Zahl ist, handelt es sich bei dem Stichproben-Median um den Wert in der Mitte. Wenn N eine gerade Zahl ist, handelt es sich bei dem Stichproben-Median um den Durchschnitt der beiden mittleren Werte.
Beispiel: Wenn N = 5 und die Daten x1, x2, x3, x4 und x5 vorliegen, ist der Median = x3.
Wenn N = 6 und die geordneten Daten x1, x2, x3, x4, x5 und x6 vorliegen:

wobei x3 und x4 die dritte und vierte Beobachtung sind.
Maximum
Der größte Wert in Ihrem Datensatz.
Anteil der beobachteten Stichprobe
Formel

Notation
| Begriff | Beschreibung |
|---|---|
| x | Anzahl der Ereignisse in der ursprünglichen Stichprobe |
| N | Anzahl der Versuche in der ursprünglichen Stichprobe |
Durchschnitt der Bootstrap-Stichprobe
Formel
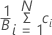
Hinweis
Beim Analysieren eines Anteils zieht Minitab keine Stichprobenwiederholungen aus der ursprünglichen Datenspalte. Stattdessen nimmt Minitab die Stichprobenwiederholungen durch Ziehen von Zufallsstichproben aus einer Binomialverteilung vor. Die Anzahl der Versuche und die Ereigniswahrscheinlichkeit für die Verteilung werden aus der ursprünglichen Stichprobe abgeleitet.
Notation
| Begriff | Beschreibung |
|---|---|
| ci | ausgewählte Statistik der i-ten Stichprobenwiederholung |
| B | Anzahl der Stichprobenwiederholungen |
| N | Anzahl der Beobachtungen in der ursprünglichen Stichprobe |
Standardabweichung der Bootstrapping-Verteilung
Formel

Notation
| Begriff | Beschreibung |
|---|---|
 | Mittelwert der ausgewählten Statistik der Stichprobenwiederholungen |
| B | Anzahl der Stichprobenwiederholungen |
| ci | ausgewählte Statistik der i-ten Stichprobenwiederholung |
Konfidenzintervall für die ausgewählte Statistik
Formel
Die ausgewählte Statistik der Stichprobenwiederholungen wird in aufsteigender Reihenfolge sortiert. x1 ist die niedrigste Zahl, xB ist die höchste Zahl.
Untergrenze: xl, wobei = 
Obergrenze: xu, wobei = 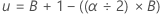
Beim Analysieren eines Anteils zieht Minitab keine Stichprobenwiederholungen aus der ursprünglichen Datenspalte. Stattdessen nimmt Minitab die Stichprobenwiederholungen durch Ziehen von Zufallsstichproben aus einer Binomialverteilung vor. Die Anzahl der Versuche und die Ereigniswahrscheinlichkeit für die Verteilung werden aus der ursprünglichen Stichprobe abgeleitet.
Hinweis
Bei einem einseitigen Test (nur Untergrenze oder nur Obergrenze) verwenden wird α anstelle von α/2 verwendet.
Wenn l oder u keine keine ganze Zahl ist, führt Minitab eine nichtlineare Interpolation zwischen den zwei Zahlen auf beiden Seiten von l oder u durch. Die Formel lautet wie folgt:
Xy + z(Xy+1 - Xy)
Wenn beispielsweise l = 5,25 ist, ist die Untergrenze gleich x5 + 0,25(x6 - x5).
In Minitab wird das Konfidenzintervall nicht angezeigt, wenn Folgendes gilt:  oder
oder 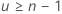 .
.
Notation
| Begriff | Beschreibung |
|---|---|
| α | 1 – Konfidenzniveau/100 |
| B | Anzahl der Stichprobenwiederholungen |
| Xy | y-te Datenzeile, wenn die Daten aufsteigend nach ihrer Größe sortiert sind |
| y | auf ganze Zahl abgeschnittener Wert von l oder u |
| z | l – y oder u – y |
