In diesem Thema
Histogramm
In einem Histogramm werden die Stichprobenwerte in eine Reihe von Intervallen unterteilt, und die Häufigkeit der Datenwerte in jedem Intervall wird in Form eines Balkens abgebildet.
Interpretation
50 Stichprobenwiederholungen
1000 Stichprobenwiederholungen
Die Verteilung lässt sich im Allgemeinen leichter mit einer höheren Anzahl von Stichprobenwiederholungen bestimmen. In diesen Daten ist die Verteilung für 50 Stichprobenwiederholungen beispielsweise mehrdeutig. Bei 1000 Stichprobenwiederholungen sieht die Form annähernd normalverteilt aus.
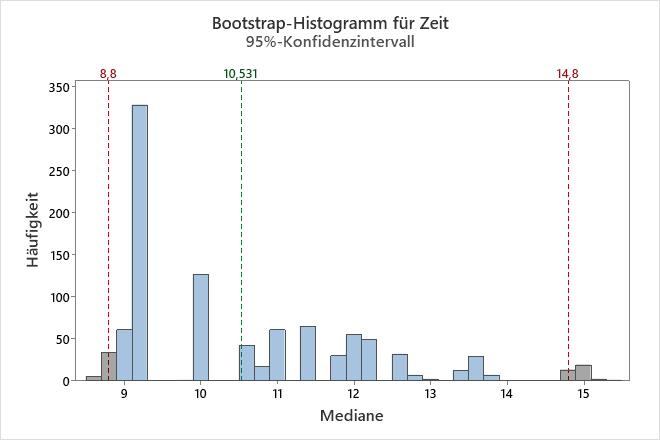
In diesem Histogramm ist die Bootstrap-Verteilung anscheinend nicht normalverteilt. Die ursprüngliche Stichprobe weist lediglich 16 Datenpunkte auf. Um ein zuverlässiges Konfidenzintervall zu erhalten, sollten Sie eine größere Stichprobe ziehen und die Analyse wiederholen.
Einzelwertdiagramm
In einem Einzelwertdiagramm werden die Einzelwerte in der Stichprobe gezeigt. Jeder Kreis stellt eine Beobachtung dar. Ein Einzelwertdiagramm ist besonders hilfreich, wenn nur eine kleine Anzahl von Beobachtungen vorliegt und Sie zudem die Auswirkung jeder Beobachtung bewerten müssen.
Hinweis
Minitab zeigt nur dann ein Einzelwertdiagramm an, wenn Sie nur eine Stichprobenwiederholung ziehen. Minitab zeigt sowohl die ursprünglichen Daten als auch die Daten aus der Stichprobenwiederholung an.
Interpretation
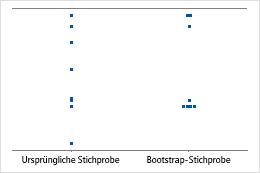
Stichprobenumfang von 8
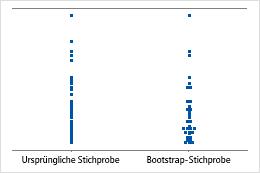
Stichprobenumfang von 50
Balkendiagramm
Im Balkendiagramm wird der Anteil an den Ereignissen für jede Kategorie angezeigt.
Hinweis
Minitab zeigt ein Balkendiagramm an, wenn Sie nur eine Stichprobenwiederholung vornehmen. Minitab zeigt sowohl die ursprünglichen Daten als auch die Daten aus der Stichprobenwiederholung an.
Interpretation
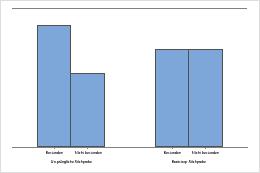
Stichprobenumfang von 8
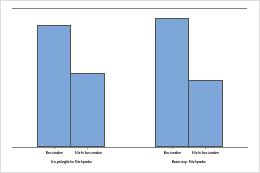
Stichprobenumfang von 50
Anzahl von Stichprobenwiederholungen
Die Anzahl der Stichprobenwiederholungen gibt die Häufigkeit an, mit der Minitab eine Zufallsstichprobe mit Zurücklegen aus dem ursprünglichen Datensatz zieht. Im Allgemeinen empfiehlt sich eine große Anzahl von Stichprobenwiederholungen. Der Stichprobenumfang für jede Stichprobenwiederholung ist gleich dem Stichprobenumfang des ursprünglichen Datensatzes. Die Anzahl der Stichprobenwiederholungen ist gleich der Anzahl der Beobachtungen im Histogramm.
Durchschnitt
Der Durchschnitt ist die Summe der ausgewählten Statistik in der Bootstrap-Stichprobe dividiert durch die Anzahl von Stichprobenwiederholungen.
Interpretation
Minitab zeigt zwei Differenzwerte der ausgewählten Statistik an, den Wert für die beobachtete Stichprobe und den Wert für die Bootstrap-Verteilung (Durchschnitt). Beide Werte stellen einen Schätzwert des Parameters der Grundgesamtheit dar und sind im Allgemeinen gleich. Besteht eine große Differenz zwischen diesen beiden Werten, empfiehlt es sich, den Stichprobenumfang der ursprünglichen Stichprobe zu vergrößern.
Da der Durchschnitt auf Stichprobendaten und nicht auf der vollständigen Grundgesamtheit basiert, ist es unwahrscheinlich, dass der Durchschnitt gleich dem Parameter der Grundgesamtheit ist. Verwenden Sie das Konfidenzintervall, um den Parameter der Grundgesamtheit besser schätzen zu können.
StdAbw (Bootstrap-Stichprobe)
Die Standardabweichung der Bootstrap-Stichproben (auch als Bootstrap-Standardfehler bezeichnet) ist ein Schätzwert der Standardabweichung der Stichprobenverteilung der ausgewählten Statistik.
Interpretation
Verwenden Sie die Standardabweichung, um zu ermitteln, wie stark die ausgewählten Statistiken aus der Bootstrap-Stichprobe um den Gesamtmittelwert gestreut sind. Ein höherer Wert der Standardabweichung verweist auf eine größere Streubreite.
Verwenden Sie die Standardabweichung der Bootstrap-Stichproben, um zu bestimmen, wie genau die Schätzwerte der Bootstrap-Statistik den Parameter der Grundgesamtheit schätzen. Ein kleinerer Wert zeigt einen präziseren Schätzwert für den Parameter der Grundgesamtheit an. Ein größerer Stichprobenumfang ergibt einen kleineren Bootstrap-Standardfehler und einen präziseren Schätzwert für den Parameter der Grundgesamtheit.
Konfidenzintervall (KI) und Konfidenzgrenzen
Konfidenzintervalle basieren auf der Stichprobenverteilung einer Statistik. Wenn eine Statistik im Hinblick auf den Schätzwert für einen Parameter nicht verzerrt ist, ist ihre Stichprobenverteilung um den wahren Wert des Parameters zentriert. Eine Bootstrapping-Verteilung entspricht annähernd der Stichprobenverteilung der Statistik. Daher liefern die mittleren 95 % der Werte aus der Bootstrapping-Verteilung ein 95%-Konfidenzintervall für den Parameter. Anhand des Konfidenzintervalls können Sie die praktische Signifikanz Ihres Schätzwerts für den Parameter der Grundgesamtheit beurteilen. Bestimmen Sie anhand Ihrer Fachkenntnisse, ob das Konfidenzintervall Werte umfasst, die in der jeweiligen Situation von praktischer Signifikanz sind.
Hinweis
Minitab berechnet kein Konfidenzintervall, wenn die Anzahl der Stichprobenwiederholungen zu klein ist, um ein genaues Konfidenzintervall zu erhalten.
Beobachtete Stichprobe
| Variable | N | Mittelwert | StdAbw | Varianz | Summe | Minimum | Median | Maximum |
|---|---|---|---|---|---|---|---|---|
| Zeit | 16 | 11,331 | 3,115 | 9,702 | 181,300 | 7,700 | 10,050 | 16,000 |
Bootstrap-Stichproben für Mittelwert
| Anzahl von Stichprobenwiederholungen | Mittelwert | StdAbw | 95%-KI für μ |
|---|---|---|---|
| 1000 | 11,3095 | 0,7625 | (9,8562; 12,8562) |
In diesen Ergebnissen beträgt der Schätzwert für den Mittelwert der Grundgesamtheit ungefähr 11,3. Sie können sich zu 95 % sicher sein, dass der Mittelwert der Grundgesamtheit zwischen annähernd 9,9 und 12,9 liegt.
