Im Wahrscheinlichkeitsnetz wird aus Ihrer Stichprobe eine geschätzte kumulative Verteilungsfunktion (CDF) abgeleitet, indem der Wert jeder Beobachtung (einschließlich der wiederholten Werte) im Vergleich zu deren geschätzter kumulativen Wahrscheinlichkeit aufgetragen wird.
Minitab berechnet die geschätzte kumulative Wahrscheinlichkeit anhand einer der folgenden Formeln, die durch die Auswahl in bestimmt wird (die Standardeinstellung ist Median-Rang). In jeder Formel entspricht n der Anzahl an Beobachtungen und i dem Rang jeder Beobachtung, wobei i = 1 für den kleinsten Wert und i = n für den größten Wert gilt.
- Median-Rang (Benard)
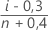
- Mittlerer Rang (Herd-Johnson)

- Kaplan-Meier modifiziert (Hazen)
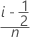
- Kaplan-Meier

Hinweis
Die Kaplan-Meier-Methode ergibt p = 1 für die größte Beobachtung. Da der resultierende Wert im Diagramm nicht verwendet werden kann, berechnet Minitab stattdessen das größte p als 90 % des Abstands zwischen dem vorausgegangenen p und 1.
Die angepasste Verteilungslinie stellt die Verteilungsfunktion (CDF) der ausgewählten theoretischen Verteilung mit den angegeben Parametern (entweder geschätzt oder historisch) dar. Wenn Sie keine historischen Parameter angeben, schätzt Minitab die Parameter mit der Schätzmethode der kleinsten Quadrate (Normal- oder Lognormalverteilung) oder der Maximum-Likelihood-Schätzmethode (andere Verteilungen).
Die y-Werte (und in einigen Fällen die x-Werte) werden transformiert, so dass die angepasste Linie linear ist. Die Teilstrichbeschriftungen entsprechen jedoch weiterhin den untransformierten Werten. Deswegen bilden die aufgetragenen Punkte eine Gerade, sofern die ausgewählte Verteilung für die Daten passend ist.
In der folgenden Tabelle werden die Transformationen aufgeführt, die für jede Verteilung verwendet werden.
| Verteilung | x-Koordinate | y-Koordinate (Score) |
|---|---|---|
| Normal | Daten | |
| Lognormal | ln(Daten) | |
| Lognormal mit 3 Parametern | ln(Daten – Schwellenwert) | |
| Gamma | ln(Daten) | G–1(p), k |
| Gamma mit 3 Parametern | ln(Daten – Schwellenwert) | G–1(p), k |
| Exponential | ln(Daten) | ln(–ln(1 – p)) |
| Exponential mit 2 Parametern | ln(Daten – Schwellenwert) | ln(–ln(1 – p)) |
| Kleinster Extremwert | Daten | ln(–ln(1 – p)) |
| Weibull | ln(Daten) | ln(–ln(1 – p)) |
| Weibull mit 3 Parametern | ln(Daten – Schwellenwert) | ln(–ln(1 – p)) |
| Größter Extremwert | Daten | –ln(–ln(p)) |
| Logistisch | Daten |
 |
| Loglogistisch | ln(Daten) |
 |
| Loglogistisch mit 3 Parametern | ln(Daten – Schwellenwert) |
 |
Wichtig
Wenn Sie Daten grafisch darstellen, die nicht für den Schwellenwert korrigiert sind, bildet die angepasste Verteilungslinie keine Gerade.
Notation
| Begriff | Beschreibung |
|---|---|
| Daten | Datenwert für die Beobachtung |
| In(x) | natürlicher Logarithmus von x |
| Der für p von der inversen Verteilungsfunktion der Standardnormalverteilung zurückgegebene Wert. | |
| G–1(p), k | Der für p durch die inverse Verteilungsfunktion der Gamma-Verteilung mit Formparameter = k und Skalenparameter = 1 zurückgegebene Wert. Minitab verwendet den geschätzten Formparameter, sofern Sie keinen historischen Wert eingeben. |
