In diesem Thema
Schritt 1: Bestimmen, ob die Daten nicht der Verteilung folgen
- p-Wert ≤ α: Die Daten folgen der Verteilung nicht (H0 zurückweisen)
- Wenn der p-Wert kleiner oder gleich dem Signifikanzniveau ist, weisen Sie die Nullhypothese zurück und schlussfolgern, dass die Daten der Verteilung nicht folgen.
- p-Wert > α: Es kann nicht gefolgert werden, dass die Daten der Verteilung nicht folgen (H0 nicht zurückweisen)
- Wenn der p-Wert größer als das Signifikanzniveau ist, weisen Sie die Nullhypothese nicht zurück, da nicht genügend Anzeichen für die Schlussfolgerung vorliegen, dass die Daten der Verteilung nicht folgen. Sie können jedoch nicht schlussfolgern, dass die Daten der Verteilung folgen.
Informationen zum Angeben anderer Verteilungen und Parameter für den Test finden Sie unter Angepasste Verteilungslinien.
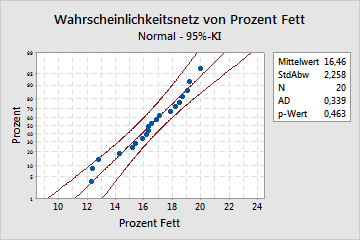
Wichtigste Ergebnisse: p-Wert
In diesen Ergebnissen besagt die Nullhypothese, dass die Daten einer Normalverteilung folgen. Da der p-Wert 0,463 beträgt und somit höher als das Signifikanzniveau von 0,05 ist, wird entschieden, die Nullhypothese nicht zu verwerfen. Sie können nicht folgern, dass die Daten keiner Normalverteilung folgen.
Achtung
Der Stichprobenumfang wirkt sich auf die Trennschärfe des Tests aus. Bei extrem kleinen Stichproben ist die Trennschärfe möglicherweise unzureichend, um signifikante Abweichungen von der Verteilung zu erkennen. Bei extrem großen Stichproben ist die Trennschärfe möglicherweise übermäßig groß, so dass geringfügige, unbedeutende Abweichungen von der Verteilung erkannt werden. Nutzen Sie daher zum Beurteilen der Verteilungsanpassung sowohl die visuelle Darstellung im Wahrscheinlichkeitsnetz als auch die p-Werte, wie in Schritt 2 beschrieben.
Schritt 2: Visualisieren der Verteilungsanpassung
Untersuchen Sie das Wahrscheinlichkeitsnetz, und beurteilen Sie, wie eng die Datenpunkte der angepassten Verteilungslinie folgen. Wenn die angegebene theoretische Verteilung eine gute Anpassung bietet, liegen die Punkte dicht entlang der Geraden. Die Punkte im folgenden Wahrscheinlichkeitsnetz für Normalverteilung liegen beispielsweise dicht an der Anpassungslinie. Die Normalverteilung scheint gut an die Daten angepasst zu sein.
Hinweis
Die angepasste Verteilungslinie ist die mittlere Gerade im Diagramm. Bei den äußeren durchgezogenen Linien im Diagramm handelt es sich um Konfidenzintervalle für die einzelnen Perzentile, nicht für die Verteilung als Ganzes; daher sollten diese nicht zur Beurteilung der Verteilungsanpassung herangezogen werden.
Weitere Informationen zur visuellen Beurteilung der Werte im Wahrscheinlichkeitsnetz finden Sie unter Wahrscheinlichkeitsnetze für Normalverteilung und der „Fat-Pencil-Test“.
Schritt 3: Anzeigen von geschätzten Perzentilen für die Grundgesamtheit
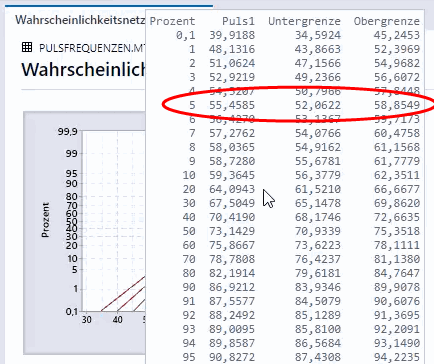
Zeigen Sie in Minitab mit dem Mauszeiger auf die angepasste Verteilungslinie, um eine Tabelle der Perzentile und Werte abzurufen.
Im folgenden Wahrscheinlichkeitsnetz werden beispielsweise die Pulsfrequenzen von Probanden beim Training auf einem Laufband veranschaulicht. Bei einer Normalverteilung mit einem Mittelwert und einer Standardabweichung, die den Daten entsprechen, ist zu erwarten, dass 5 % der Grundgesamtheit eine Pulsfrequenz von höchstens 54,76 aufweisen.
Hinweis
Die geschätzten Perzentile für die Grundgesamtheit sind nur genau, wenn die Daten der Verteilung eng folgen.
