In diesem Thema
- Kumulative Verteilungsfunktion
- Inverse kumulative Wahrscheinlichkeit
- Dichtefunktion
- Betaverteilung
- Binomialverteilung
- Cauchy-Verteilung
- Chi-Quadrat-Verteilung
- Diskrete Verteilung
- Exponentialverteilung
- F-Verteilung
- Gamma-Verteilung
- Geometrische Verteilung
- Hypergeometrische Verteilung
- Ganzzahlige Verteilung
- Laplace-Verteilung
- Verteilung des größten Extremwerts
- Logistische Verteilung
- Loglogistische Verteilung
- Lognormale Verteilung
- Negative Binomialverteilung
- Normalverteilung
- Poisson-Verteilung
- Verteilung des kleinsten Extremwerts
- t-Verteilung
- Dreiecksverteilung
- Gleichverteilung
- Weibull-Verteilung
Kumulative Verteilungsfunktion
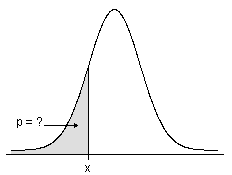
- Für stetige Verteilungen gibt die CDF die Fläche unter der Dichtefunktion bis zu dem von Ihnen angegebenen x-Wert an.
- Für diskrete Verteilungen gibt die CDF die kumulative Wahrscheinlichkeit für von Ihnen angegebene X-Werte an.
Inverse kumulative Wahrscheinlichkeit
Für eine Anzahl p in dem geschlossenen Intervall [0,1] bestimmt die inverse kumulative Verteilungsfunktion (ICDF) einer Zufallsvariable X wenn möglich einen Wert x, für den gilt, dass die Wahrscheinlichkeit von X ≤ x größer als oder gleich p ist.
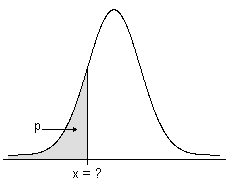
- ICDF für stetige Verteilungen
-
Die ICDF ist der Wert, der einer Fläche unter der Dichtefunktion entspricht. Die ICDF ist die Umkehrung der kumulativen Verteilungsfunktion (CDF); diese ist die Fläche, die einem Wert entspricht.
Die ICDF ist für alle stetigen Verteilungen definiert und eindeutig, wenn 0 < p < 1 ist.
- Wenn die Dichtefunktion (PDF) für die gesamte Reihe reeller Zahlen positiv ist (z. B. die PDF der Normalverteilung), ist die ICDF weder für p = 0 noch für p = 1 definiert.
- Wenn die PDF für alle Werte größer als ein bestimmter Wert positiv ist (z. B. die PDF für die Chi-Quadrat-Verteilung), ist die ICDF für p = 0 definiert, aber nicht für p = 1.
- Wenn die PDF nur für ein Intervall positiv ist (z. B. die PDF für die Gleichverteilung), ist die ICDF für p = 0 und p = 1 definiert.
- Wenn die ICDF nicht definiert ist, gibt Minitab als Ergebnis einen fehlenden Wert (*) zurück.
- ICDF für diskrete Verteilungen
- Bei diskreten Verteilungen ist die CDF komplizierter als für stetige Verteilungen. Wenn Sie die CDF für eine Binomialverteilung mit beispielsweise n = 5 und p = 0,4 berechnen, gibt es keinen x-Wert, für den die CDF 0,5 ist. Für x = 1 ist die CDF 0,3370. Für x = 2 steigt die CDF auf 0,6826.
Dichtefunktion
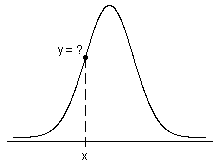
- Für stetige Verteilungen entspricht die Wahrscheinlichkeit, dass X in einem Intervall (a; b) Werte aufweist, exakt der Fläche unter der zugehörigen PDF im Intervall (a; b).
- Für stetige Verteilungen entspricht die Wahrscheinlichkeit, dass X in einem Intervall (a; b) Werte aufweist, exakt der Summe der PDF (auch als Wahrscheinlichkeitsfunktion bekannt) der möglichen diskreten Werte von X in (a; b).
Betaverteilung
Die Betaverteilung wird häufig zur Darstellung von Prozessen mit natürlichen Unter- und Obergrenzen verwendet.
Formel
Die Dichtefunktion (PDF) lautet:

Notation
| Begriff | Beschreibung |
|---|---|
| α | Formparameter 1 |
| β | Formparameter 2 |
| Γ | Gamma-Funktion |
| a | Untergrenze |
| b | Obergrenze |
Wenn a = 0 und b = 1,
lautet die PDF:
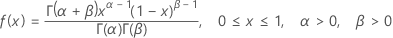


Binomialverteilung
Mit der Binomialverteilung wird dargestellt, wie häufig Ereignisse in n unabhängigen Versuchen eintreten. Mögliche Werte sind ganze Zahlen von null bis n.
Formel
Mittelwert = np
Varianz = np(1 – p)
Die Wahrscheinlichkeitsfunktion (PMF) lautet:
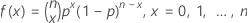
Hierbei ist  gleich
gleich  .
.
In der Regel kann k! berechnet werden als 
Notation
| Begriff | Beschreibung |
|---|---|
| n | Anzahl der Versuche |
| x | Anzahl der Ereignisse |
| p | Ereigniswahrscheinlichkeit |
Cauchy-Verteilung
Die Cauchy-Verteilung ist um null symmetrisch, doch nähern sich die Randbereiche langsamer dem Wert null als bei einer Normalverteilung.
Formel
Die Dichtefunktion (PDF) lautet:
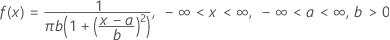
Notation
| Begriff | Beschreibung |
|---|---|
| a | Lageparameter |
| b | Skalenparameter |
| π | Pi (~3,142) |
Hinweis
Wenn Sie keine Werte angeben, verwendet Minitab a = 0 and b = 1.
Chi-Quadrat-Verteilung
Wenn x eine Standardnormalverteilung aufweist, weist x2 eine Chi-Quadrat-Verteilung mit einem Freiheitsgrad auf; diese Verteilung wird daher häufig als Stichprobenverteilung verwendet.
Die Summe von n unabhängigen x2-Variablen (wobei x eine Standardnormalverteilung aufweist) weist eine Chi-Quadrat-Verteilung mit n Freiheitsgraden auf. Die Form der Chi-Quadrat-Verteilung hängt von der Anzahl der Freiheitsgrade ab.
Formel
Die Dichtefunktion (PDF) lautet:
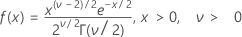
Mittelwert = v
Varianz = 2v
Notation
| Begriff | Beschreibung |
|---|---|
| ν | Freiheitsgrade |
| Γ | Gamma-Funktion |
| e | Basis des natürlichen Logarithmus |
Diskrete Verteilung
Eine diskrete Verteilung definieren Sie selbst. Angenommen, Sie untersuchen eine Verteilung, die aus den drei Werten -1, 0 und 1 besteht, denen die Wahrscheinlichkeiten 0,2; 0,5 bzw. 0,3 entsprechen. Wenn Sie die Werte in die Spalten eines Arbeitsblatts eingeben, können Sie anhand dieser Spalten Zufallszahlen erzeugen oder Wahrscheinlichkeiten berechnen.
| Wert | Wahrsch |
|---|---|
| −1 | 0,2 |
| 0 | 0,5 |
| 1 | 0,3 |
Exponentialverteilung
Mit der Exponentialverteilung lassen sich Zeiten zwischen Ausfällen modellieren, z. B. wenn Einheiten eine konstante momentane Ausfallrate aufweisen (Hazard-Funktion). Bei der Exponentialverteilung handelt es sich um einen Sonderfall der Weibull-Verteilung und der Gammaverteilung.
Formel
Die Dichtefunktion (PDF) lautet:
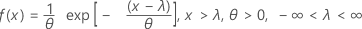
Die kumulative Verteilungsfunktion (CDF) lautet:

Mittelwert = θ + λ
Varianz = θ2
Notation
| Begriff | Beschreibung |
|---|---|
| θ | Skalenparameter |
| λ | Schwellenwertparameter |
| exp | Basis des natürlichen Logarithmus |
Hinweis
In der Literatur wird für den Parameter zum Teil „1/θ“ gebraucht.
F-Verteilung
Die F-Verteilung wird auch als Verteilung des Varianz-Verhältnisses bezeichnet; sie weist zwei Typen von Freiheitsgraden auf: Freiheitsgrade des Zählers und Freiheitsgrade des Nenners. Sie stellt die Verteilung des Verhältnisses zwischen zwei unabhängigen Zufallsvariablen mit Chi-Quadrat-Verteilungen jeweils dividiert durch ihre Freiheitsgrade dar.
Formel
Die Dichtefunktion (PDF) lautet:
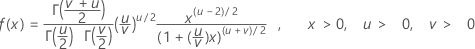

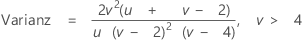
Notation
| Begriff | Beschreibung |
|---|---|
| Γ | Gamma-Funktion |
| u | Freiheitsgrade des Zählers |
| v | Freiheitsgrade des Nenners |
Gamma-Verteilung
Mit der Gamma-Verteilung werden häufig positiv schiefe Daten modelliert.
Formel
Die Dichtefunktion (PDF) lautet:

Mittelwert = ab + θ
Varianz = ab2
Notation
| Begriff | Beschreibung |
|---|---|
| a | Formparameter (bei a = 1 entspricht die PDF für die Gamma-Verteilung der PDF für die Exponentialverteilung) |
| b | Skalenparameter |
| θ | Schwellenwertparameter |
| Γ | Gamma-Funktion |
| e | Basis des natürlichen Logarithmus |
Hinweis
In der Literatur wird für den Parameter zum Teil „1/b“ gebraucht.
Geometrische Verteilung
Die diskrete geometrische Verteilung gilt für eine Folge unabhängiger Bernoulli-Experimente mit einem Ereignis von Interesse, dessen Wahrscheinlichkeit p beträgt.
Formel
Wenn die Zufallsvariable x der Gesamtzahl der erforderlichen Versuche entspricht, um ein Ereignis mit der Wahrscheinlichkeit p zu erhalten, wird die Wahrscheinlichkeitsfunktion (PMF) von x angegeben als:

und x weist folgende Eigenschaften auf:


Wenn die Zufallsvariable y der Anzahl der auftretenden Nicht-Ereignisse entspricht, bevor das erste Ereignis (mit der Wahrscheinlichkeit p) beobachtet wird, wird die Wahrscheinlichkeitsfunktion (PMF) von y angegeben als:

und y weist folgende Eigenschaften auf:


Notation
| Begriff | Beschreibung |
|---|---|
| X | Anzahl der zum Auslösen eines einzelnen Ereignisses benötigten Versuche, Y + 1 |
| Y | Anzahl der Nicht-Ereignisse, die vor dem ersten Ereignis auftreten |
| p | Wahrscheinlichkeit, dass bei einem Versuch ein Ereignis eintritt |
Hypergeometrische Verteilung
Die hypergeometrische Verteilung wird für Stichproben verwendet, die ohne Zurücklegen aus kleinen Grundgesamtheiten entnommen werden. Angenommen, bei einer Lieferung von N Fernsehgeräten sind N1 gut (Erfolge) und N2 fehlerhaft (Ausfälle). Wenn Sie eine Zufallsstichprobe von n aus N Fernsehgeräten ohne Zurücklegen entnehmen, können Sie die Wahrscheinlichkeit ermitteln, dass genau x der n Fernsehgeräte gut sind.
Formel
Die Wahrscheinlichkeitsfunktion (PMF) lautet:
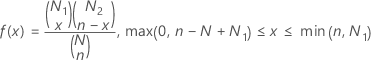
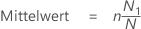

Notation
| Begriff | Beschreibung |
|---|---|
| N | N1 + N2 = Größe der Grundgesamtheit |
| N1 | Anzahl der Ereignisse in der Grundgesamtheit |
| N2 | Anzahl der Nicht-Ereignisse in der Grundgesamtheit |
| n | Stichprobenumfang |
| x | Anzahl der Ereignisse in der Stichprobe |
Ganzzahlige Verteilung
Die ganzzahlige Verteilung ist eine diskrete Gleichverteilung für eine Menge von ganzen Zahlen. Jede ganze Zahl weist die gleiche Vorkommenswahrscheinlichkeit auf.
Laplace-Verteilung
Die Laplace-Verteilung wird verwendet, wenn die Verteilung eine stärkere Spitze als eine Normalverteilung aufweist.
Formel
Die Dichtefunktion (PDF) lautet:
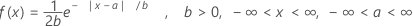
Mittelwert = a
Varianz = 2b2
Notation
| Begriff | Beschreibung |
|---|---|
| a | Lageparameter |
| b | Skalenparameter |
| e | Basis des natürlichen Logarithmus |
Verteilung des größten Extremwerts
Verwenden Sie die Verteilung des größten Extremwerts zum Modellieren des größten Werts einer Verteilung. Wenn eine Folge von Exponentialverteilungen vorliegt und x(n) das Maximum der ersten n Verteilungen ist, dann nähert sich die Verteilung von x(n) – ln(n) der Verteilung des größten Extremwerts an. Bei großen Werten von n stellt die Verteilung des größten Extremwerts daher eine gute Annäherung an die Verteilung von x(n) – ln(n) dar.
Formel
Die Dichtefunktion (PDF) lautet:

Die kumulative Verteilungsfunktion (CDF) lautet:

Mittelwert = μ + γσ
Varianz = π 2 σ 2 / 6
Notation
| Begriff | Beschreibung |
|---|---|
| σ | Skalenparameter |
| μ | Lageparameter |
| γ | Euler-Konstante (~0,57722) |
Logistische Verteilung
Eine stetige Verteilung, die symmetrisch ist und der Normalverteilung ähnelt, aber stärker besetzte Randbereiche aufweist.
Formel
Die Dichtefunktion (PDF) lautet:
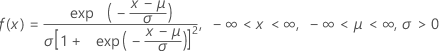
Die kumulative Verteilungsfunktion (CDF) lautet:
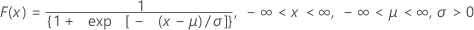
Mittelwert = μ
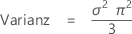
Notation
| Begriff | Beschreibung |
|---|---|
| μ | Lageparameter |
| σ | Skalenparameter |
Loglogistische Verteilung
Eine Variable x weist eine loglogistische Verteilung mit dem Schwellenwert λ auf, wenn Y = log (x – λ) eine logistische Verteilung aufweist.
Formel
Die Dichtefunktion (PDF) lautet:
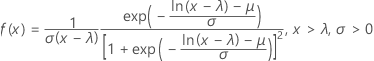
Die kumulative Verteilungsfunktion (CDF) lautet:

wenn σ < 1:
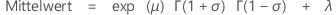
wenn σ < 1/2:
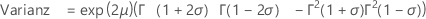
Notation
| Begriff | Beschreibung |
|---|---|
| μ | Lageparameter |
| σ | Skalenparameter |
| λ | Schwellenwertparameter |
| Γ | Gamma-Funktion |
| exp | Basis des natürlichen Logarithmus |
Lognormale Verteilung
Eine Variable x weist eine lognormale Verteilung auf, wenn log(x – λ) eine Normalverteilung aufweist.
Formel
Die Dichtefunktion (PDF) lautet:

Die kumulative Verteilungsfunktion (CDF) lautet:


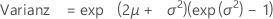
Notation
| Begriff | Beschreibung |
|---|---|
| μ | Lageparameter |
| σ | Skalenparameter |
| λ | Schwellenwertparameter |
| π | Pi (~3,142) |
Negative Binomialverteilung
Die diskrete negative Binomialverteilung gilt für eine Folge unabhängiger Bernoulli-Experimente mit einem Ereignis von Interesse, dessen Wahrscheinlichkeit p beträgt.
Formel



Wenn die Zufallsvariable y der Anzahl der auftretenden Nicht-Ereignisse entspricht, bevor Sie r Ereignisse beobachten, die jeweils die Wahrscheinlichkeit p aufweisen, wird die Wahrscheinlichkeitsfunktion (PMF) von y angegeben durch:
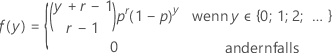
und y weist folgende Eigenschaften auf:


Hinweis
Diese negative Binomialverteilung ist auch als Pascal-Verteilung bekannt.
Notation
| Begriff | Beschreibung |
|---|---|
| x | y + r |
| r | Anzahl der Ereignisse |
| p | Ereigniswahrscheinlichkeit |
Normalverteilung
Die Normalverteilung (auch als auch als Gaußsche Verteilung bezeichnet) ist die am häufigsten verwendete statistische Verteilung, da sie viele physikalische, biologische und soziale Prozesse modellieren kann.
Formel
Die Dichtefunktion (PDF) lautet:
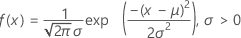
Die kumulative Verteilungsfunktion (CDF) lautet:
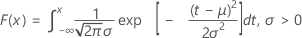
Mittelwert = μ
Varianz = σ 2
Standardabweichung = σ
Notation
| Begriff | Beschreibung |
|---|---|
| exp | Basis des natürlichen Logarithmus |
| π | Pi (~3,142) |
Poisson-Verteilung
Die Poisson-Verteilung ist eine diskrete Verteilung, die die Anzahl der Ereignisse auf der Grundlage einer konstanten Ereignisrate modelliert. Die Poisson-Verteilung kann als Annäherung an die Binomialverteilung verwendet werden, wenn die Anzahl der unabhängigen Versuche groß und die Wahrscheinlichkeit eines Erfolgs gering ist.
Formel
Die Wahrscheinlichkeitsfunktion (PMF) lautet:
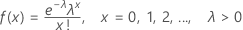
Mittelwert = λ
Varianz = λ
Notation
| Begriff | Beschreibung |
|---|---|
| e | Basis des natürlichen Logarithmus |
Verteilung des kleinsten Extremwerts
Verwenden Sie die Verteilung des kleinsten Extremwerts, um den kleinsten Wert einer Verteilung zu modellieren. Wenn y der Weibull-Verteilung folgt, folgt log(y) der Verteilung des kleinsten Extremwerts.
Formel
Die Dichtefunktion (PDF) lautet:
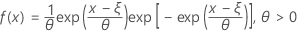
Die kumulative Verteilungsfunktion (CDF) lautet:

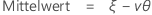

Notation
| Begriff | Beschreibung |
|---|---|
| ξ | Lageparameter |
| θ | Skalenparameter |
| e | Basis des natürlichen Logarithmus |
| v | Euler-Konstante (~0,57722) |
t-Verteilung
- Erstellen von Konfidenzintervallen für den Mittelwert einer Grundgesamtheit aus einer Normalverteilung, wenn die Varianz unbekannt ist
- Bestimmen, ob sich zwei Stichproben-Mittelwerte aus normalverteilten Grundgesamtheiten mit unbekannten, aber gleichen Varianzen signifikant unterscheiden
- Testen der Signifikanz von Regressionskoeffizienten
Formel
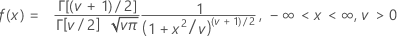
Mittelwert = 0, wenn ν > 0

Notation
| Begriff | Beschreibung |
|---|---|
| Γ | Gamma-Funktion |
| v | Freiheitsgrade |
| π | Pi (~3,142) |
Dreiecksverteilung
Die PDF der Dreiecksverteilung weist eine dreieckige Form auf.
Formel
Die Dichtefunktion (PDF) lautet:
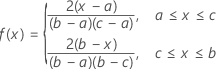

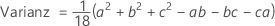
Notation
| Begriff | Beschreibung |
|---|---|
| a | unterer Endpunkt |
| b | oberer Endpunkt |
| c | Modalwert (Lage der Spitze der PDF) |
Gleichverteilung
Mit der Gleichverteilung werden in einem Intervall gleichmäßig angeordnete Daten charakterisiert, wobei a der kleinste und b der größte Wert ist.
Formel
Die Dichtefunktion (PDF) lautet:


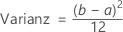
Notation
| Begriff | Beschreibung |
|---|---|
| a | unterer Endpunkt |
| b | oberer Endpunkt |
Weibull-Verteilung
Die Weibull-Verteilung wird zum Modellieren von Produktausfallzeiten verwendet.
Formel
Die Dichtefunktion (PDF) lautet:
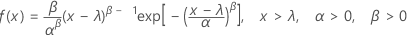
Die kumulative Verteilungsfunktion (CDF) lautet:


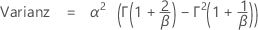
Notation
| Begriff | Beschreibung |
|---|---|
| α | Skalenparameter |
| β | Formparameter, bei β = 1 entspricht die PDF für die Weibull-Verteilung der PDF für die Exponentialverteilung |
| λ | Schwellenwertparameter |
| Γ | Gamma-Funktion |
| exp | Basis des natürlichen Logarithmus |
Hinweis
In der Literatur wird für den Parameter zum Teil „1/α“ gebraucht.
