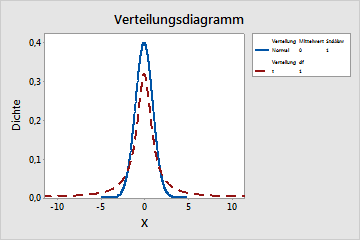
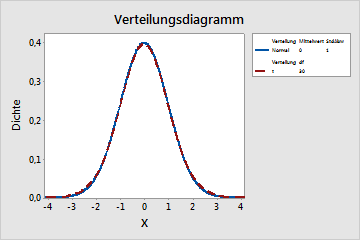
Ein Statistiker möchte die Beziehung zwischen der t-Verteilung und der Standardnormalverteilung veranschaulichen. Bei der Standardnormalverteilung handelt es sich um eine Normalverteilung mit Mittelwert = 0 und Standardabweichung = 1. Bei der t-Verteilung wird davon ausgegangen, dass sie sich bei zunehmender Anzahl von Freiheitsgraden an die Standardnormalverteilung annähert.
- Wählen Sie aus.
- Wählen Sie Zwei Verteilungen aus, und klicken Sie dann auf OK.
- Wählen Sie im Feld Verteilung 1 die Option t aus.
- Geben Sie im Feld Freiheitsgrade den Wert 1 ein.
- Wählen Sie im Feld Verteilung 2 die Option Normal aus.
- Geben Sie im Feld MWert den Wert 0 ein. Geben Sie im Feld Standardabweichung den Wert 1 ein.
- Klicken Sie auf OK.
- Wiederholen Sie die Schritte 1 bis 7, geben Sie jedoch in Schritt 4 für die t-Verteilung 30 Freiheitsgrade an, um die zweite Grafik zu erstellen.
Interpretieren der Ergebnisse
Bei einem Freiheitsgrad ähnelt die t-Verteilung in ihrer Form der Standardnormalverteilung; die t-Verteilung weist jedoch größere Randbereiche auf. Bei 30 Freiheitsgraden stimmt die t-Verteilung annähernd mit der Standardnormalverteilung überein.