In diesem Thema
Schritt 1: Auswerten der wesentlichen Merkmale
Untersuchen Sie die Lage und die Streubreite der Verteilung. Werten Sie aus, inwiefern sich der Stichprobenumfang auf das Aussehen des Einzelwertdiagramms auswirkt.
Lage und Streubreite
Ermitteln Sie die dichtesten Cluster von Symbolen. Die dichtesten Cluster stellen die am häufigsten auftretenden Werte dar. Werten Sie die Streubreite der einzelnen Gruppen aus, um festzustellen, wie stark die Daten variieren. Zeigen Sie mit dem Mauszeiger auf einen Punkt, um eine QuickInfo einzublenden, in der die Beobachtung beschrieben wird.
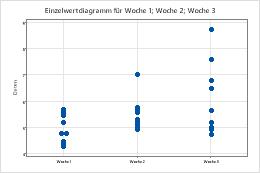
Untersuchen Sie alle unerwarteten oder unerwünschten Merkmale im Einzelwertdiagramm. In einem Einzelwertdiagramm der Härtemesswerte für eine Lieferung von Kugellagern ist beispielsweise eine außergewöhnlich breite Streubreite der Werte zu beobachten. In einer Untersuchung wurde festgestellt, dass der Anstieg der Streuung durch eine Änderung im Fertigungsprozess der Kugellager verursacht wurde.
Stichprobenumfang (n)
Der Stichprobenumfang kann sich auf das Erscheinungsbild der Grafik auswirken.
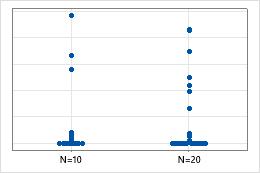
Ein Einzelwertdiagramm ist am besten geeignet, wenn der Stichprobenumfang kleiner als ungefähr 50 ist. Wenn die Stichprobe zu groß ist, liegen die Datenpunkte im Diagramm möglicherweise zu dicht beieinander, und die Verteilung kann nur schwer beurteilt werden. Erwägen Sie bei einem Stichprobenumfang größer als 50, stattdessen ein Boxplot oder ein Histogramm zu verwenden.
Schritt 2: Suchen nach Anzeichen von nicht normalverteilten oder ungewöhnlichen Daten
Schiefe Daten und multimodale Daten weisen darauf hin, dass die Daten möglicherweise nicht normalverteilt sind. Ausreißer können auf andere Bedingungen in den Daten hinweisen.
Schiefe Daten
Ermitteln Sie, ob Ihre Daten schief sind. Wenn die Daten schief sind, liegen die meisten Datenwerte am oberen oder unteren Rand der Grafik. Schiefe weist darauf hin, dass die Daten möglicherweise nicht normalverteilt sind. Häufig lässt sich die Schiefe am einfachsten mit einem Histogramm oder einem Boxplot erkennen.
Diese Einzelwertdiagramme veranschaulichen schiefe Daten. Das Einzelwertdiagramm mit rechtsschiefen Daten zeigt Wartezeiten. Die meisten Wartezeiten sind relativ kurz, und nur wenige Wartezeiten sind lang. Das Einzelwertdiagramm mit linksschiefen Daten zeigt Ausfallzeiten. Nur wenige Elemente fallen sofort aus, während viel mehr Elemente zu späteren Zeitpunkten ausfallen.
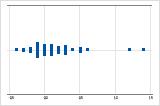
Rechtsschief

Linksschief
Wenn Ihnen bekannt ist, dass die Daten nicht naturgemäß schief sind, untersuchen Sie die möglichen Ursachen. Wenn Sie erheblich schiefe Daten analysieren möchten, lesen Sie den Artikel mit Überlegungen zu Daten für die Analyse, um sicherzustellen, dass Sie nicht normalverteilte Daten verwenden können.
Ausreißer
Ausreißer, d. h. Datenwerte, die weit entfernt von den anderen Datenwerten liegen, können sich stark auf Ihre Ergebnisse auswirken.
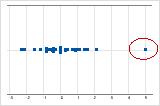
Hinweis
Zeigen Sie mit dem Mauszeiger auf den Ausreißer, um den Datenpunkt zu identifizieren.
Versuchen Sie, die Ursache von Ausreißern zu ermitteln. Korrigieren Sie sämtliche Dateneingabefehler. Erwägen Sie, Datenwerte zu entfernen, die auf ungewöhnliche, einmalige Ereignisse (Ausnahmebedingungen) zurückzuführen sind. Wiederholen Sie anschließend die Analyse.
Multimodale Daten
Multimodale Daten weisen mehrere Cluster auf, die auch als Modalwerte bezeichnet werden. Multimodale Daten deuten oftmals darauf hin, dass wichtige Variablen noch nicht berücksichtigt wurden.
Diese Einzelwertdiagramme stellen beispielsweise Grafiken der gleichen Daten dar. Das einfache Einzelwertdiagramm weist zwei Cluster auf, die Bedeutung der Cluster ist jedoch unklar. Im Einzelwertdiagramm mit Gruppen wird veranschaulicht, dass die Cluster zwei Gruppen entsprechen.
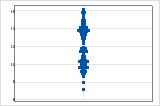
Einfach
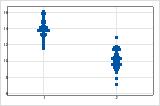
Mit Gruppen
Wenn Sie über zusätzliche Informationen verfügen, die es Ihnen ermöglichen, die Beobachtungen in Gruppen zu gliedern, können Sie anhand dieser Informationen eine Gruppierungsvariable anlegen. Dann können Sie die Grafik mit den Gruppen erstellen, um zu ermitteln, ob die Gruppierungsvariable die Spitzen in den Daten erklärt.
Tipp
Um eine Gruppierungsvariablen zu einer vorhandenen Grafik hinzuzufügen, doppelklicken Sie auf eine Datendarstellung in der Grafik, und klicken Sie anschließend auf die Registerkarte Gruppen.
Schritt 3: Auswerten und Vergleichen von Gruppen
Wenn das Einzelwertdiagramm Gruppen aufweist, beurteilen und vergleichen Sie Lage und Streubreite der Gruppen.
Lagen
Suchen Sie nach Differenzen zwischen den Lagen der Gruppen.
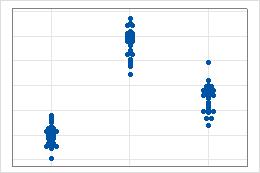
- Führen Sie einen t-Test bei zwei Stichproben aus, wenn nur zwei Gruppen vorhanden sind.
- Führen Sie eine einfache ANOVA aus, wenn drei oder mehr Gruppen vorhanden sind.
Streubreiten
Suchen Sie nach Differenzen zwischen den Streubreiten der Gruppen.
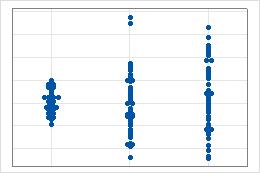
- Führen Sie einen Test auf Varianzen bei zwei Stichproben aus, wenn nur zwei Gruppen vorhanden sind.
- Führen Sie einen Test auf gleiche Varianzen aus, wenn drei oder mehr Gruppen vorhanden sind.
