Exponentialverteilung
Verwenden Sie die Exponentialverteilung, um die Zeit zwischen Ereignissen in einem stetigen Poisson-Prozess zu modellieren. Es wird davon ausgegangen, dass unabhängige Ereignisse mit einer konstanten Rate auftreten.
Diese Verteilung dient einer Vielzahl von Anwendungen, beispielsweise für Zuverlässigkeitsanalysen für Produkte und Systeme, Warteschlangentheorie und Markov-Ketten.
- Dauer bis zum Ausfall elektronischer Komponenten
- Zeitintervall zwischen dem Eintreffen von Kunden an einem Terminal
- Zeit bis zur Beratung von Kunden in der Warteschlange
- Zeit bis zum Eintreten von Zahlungsverzug (Modellierung des Kreditrisikos)
- Zeit bis zum Zerfall eines radioaktiven Atomkerns
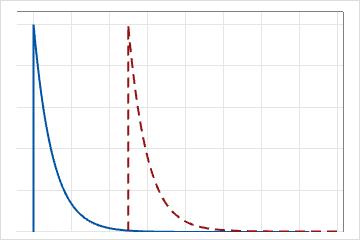
Für die Exponentialverteilung mit 1 Parameter ist der Schwellenwert 0, und die Verteilung wird durch ihren Skalenparameter definiert. Bei der Exponentialverteilung mit 1 Parameter ist der Skalenparameter gleich dem Mittelwert.
Was bedeutet „Erinnerungslosigkeit“?
Die Exponentialverteilung zeichnet sich durch die wichtige Eigenschaft der „Erinnerungslosigkeit“ aus. Die Wahrscheinlichkeit eines Ereignisses hängt nicht von vergangenen Versuchen ab. Daher bleibt die Ereignisrate konstant.
„Erinnerungslosigkeit“ bedeutet, dass die verbleibende Lebensdauer einer Komponente unabhängig von ihrem gegenwärtigen Alter ist. Die Eigenschaft der Erinnerungslosigkeit wird z. B. durch zufällige Versuche eines Münzwurfs demonstriert. Im Gegensatz dazu ist ein System, das dem Verschleiß unterliegt und daher mit steigender Lebensdauer eine höhere Ausfallwahrscheinlichkeit hat, nicht „erinnerungslos“.
Gamma-Verteilung
Verwenden Sie die Gamma-Verteilung zum Modellieren positiver Datenwerte, die rechtsschief und größer als 0 sind. Die Gamma-Verteilung kommt häufig in Zuverlässigkeits- und Lebensdaueranalysen zur Anwendung. Mit der Gamma-Verteilung können Sie zum Beispiel die Zeit bis zum Ausfall einer elektrischen Komponente beschreiben. Die meisten elektrischen Komponenten eines bestimmten Typs weisen etwa dieselbe Ausfallzeit auf, einige fallen hingegen erst nach einer langen Zeit aus.
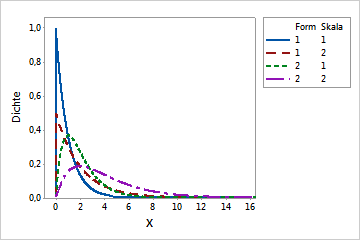
Wenn der Formparameter eine ganze Zahl ist, wird die Gamma-Verteilung gelegentlich auch als Erlang-Verteilung bezeichnet. Die Erlang-Verteilung wird oft in Anwendungen der Warteschlangentheorie verwendet.
Logistische Verteilung
Verwenden Sie die logistische Verteilung, um Datenverteilungen zu modellieren, deren Randbereiche länger und deren Kurtosis größer sind als bei der Normalverteilung.
- Effekt des Skalenparameters
- Die folgende Grafik zeigt den Effekt unterschiedlicher Werte für den Skalenparameter auf die logistische Verteilung.
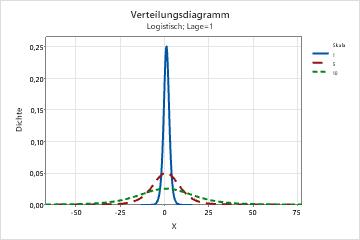
- Effekt des Lageparameters
- Die folgende Grafik zeigt den Effekt unterschiedlicher Werte für den Lageparameter auf die logistische Verteilung.
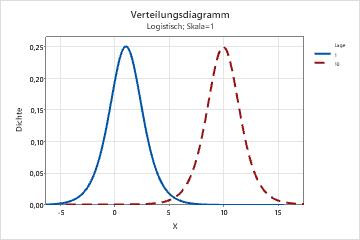
Loglogistische Verteilung
Verwenden Sie die loglogistische Verteilung, wenn der Logarithmus der Variablen logistisch verteilt ist. Die loglogistische Verteilung wird z. B. in Wachstumsmodellen und zum Modellieren binärer Antwortvariablen in Bereichen wie Biostatistik und Wirtschaft verwendet.
Bei der loglogistischen Verteilung handelt es sich um eine stetige Verteilung, die durch ihre Skalen- und Lageparameter definiert ist. Die loglogistische Verteilung mit 3 Parametern wird durch ihre Skalen-, Lage- und Schwellenwertparameter definiert.
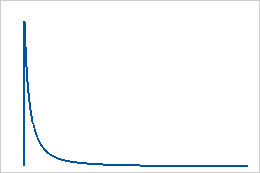
Die loglogistische Verteilung ist auch als Fisk-Verteilung bekannt.
Lognormale Verteilung
Verwenden Sie die lognormale Verteilung, wenn der Logarithmus der Zufallsvariablen normalverteilt ist. Diese Verteilung wird verwendet, wenn Zufallsvariablen größer als 0 sind. Die lognormale Verteilung wird z. B. für Zuverlässigkeitsanalysen und im Finanzbereich verwendet, beispielsweise zur Modellierung des Aktienverhaltens.
Bei der lognormalen Verteilung handelt es sich um eine stetige Verteilung, die durch ihre Lage- und Skalenparameter definiert wird. Die lognormale Verteilung mit 3 Parametern wird durch ihre Lage-, Skalen- und Schwellenwertparameter definiert.
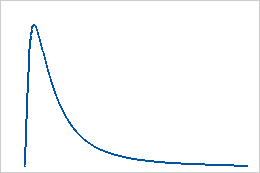
Normalverteilung
Bei der Normalverteilung handelt es sich um eine stetige Verteilung, die durch den Mittelwert (μ) und die Standardabweichung (σ) definiert ist. Der Mittelwert ist der Gipfel bzw. das Zentrum der glockenförmigen Kurve. Die Standardabweichung bestimmt die Streuung der Verteilung.
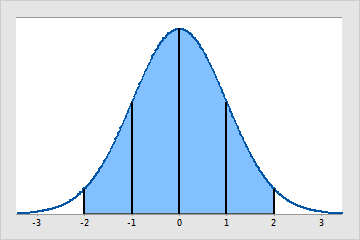
Die Normalverteilung ist die am häufigsten verwendete statistische Verteilung, da sich bei vielen physikalischen, biologischen und sozialen Untersuchungen natürlicherweise eine angenäherte Normalverteilung ergibt. Bei vielen statistischen Analysen wird davon ausgegangen, dass die Daten aus einer annähernd normalverteilten Grundgesamtheit stammen.
Verteilung des größten und des kleinsten Extremwerts
Die Verteilungen des größten und des kleinsten Extremwerts sind eng miteinander verwandt. Wenn z. B. x eine Verteilung des größten Extremwerts aufweist, dann weist –x eine Verteilung des kleinsten Extremwerts auf und umgekehrt.
Verteilung des kleinsten Extremwerts
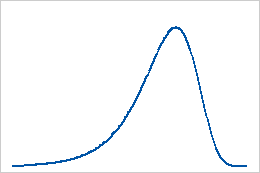
Verteilung des größten Extremwerts
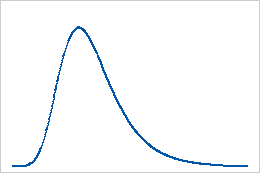
Weibull-Verteilung
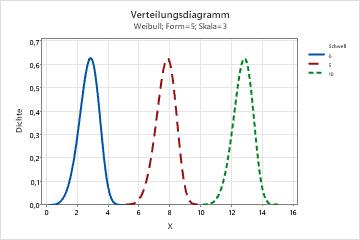
Die Weibull-Verteilung ist eine vielseitige Verteilung, die sich zum Modellieren einer Vielzahl an Anwendungen in den Bereichen Technik, medizinische Forschung, Qualitätskontrolle, Finanzen und Klimatologie eignet. Diese Verteilung wird z. B. häufig in Zuverlässigkeitsanalysen verwendet, um Daten zu Ausfallzeiten zu modellieren. Die Weibull-Verteilung wird auch zum Modellieren von schiefen Prozessdaten in Prozessfähigkeitsanalysen verwendet.
Die Weibull-Verteilung wird durch die Form-, Skalen und Schwellenwertparameter beschrieben und wird auch als Weibull-Verteilung mit 3 Parametern bezeichnet. Der Fall, in dem der Schwellenwertparameter null ist, wird als Weibull-Verteilung mit 2 Parametern bezeichnet. Die Weibull-Verteilung mit 2 Parametern ist nur für positive Variablen definiert. Bei einer Weibull-Verteilung mit 3 Parametern sind Nullwerte und negativen Daten zulässig, die Daten für eine Weibull-Verteilung mit 2 Parametern müssen jedoch größer als null sein.
Je nach den Werten der Parameter kann die Weibull-Verteilung verschiedene Formen annehmen.
- Effekt des Formparameters
- Der Formparameter beschreibt, wie Ihre Daten verteilt sind. Eine Form von 3 ist annähernd eine Normalverteilungskurve. Ein geringer Wert für die Form wie 1 ergibt eine rechtsschiefe Kurve. Ein hoher Wert für die Form wie 10 führt zu einer linksschiefen Kurve.
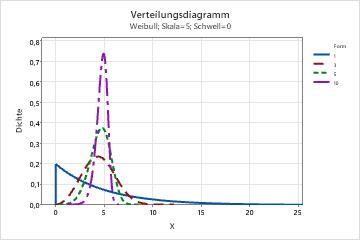
- Effekt des Skalenparameters
- Die Skala bzw. die charakteristische Lebensdauer ist das 63,2-te Perzentil der Daten. Die Skala definiert die Position der Weibull-Kurve relativ zum Schwellenwert; dies ist vergleichbar mit der Art, wie der Mittelwert die Position einer Normalverteilungskurve definiert. Eine Skala von 20 gibt beispielsweise an, dass 63,2 % der Geräte in den ersten 20 Stunden nach der Schwellenwertzeit ausfallen werden.
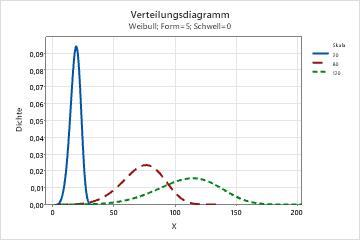
- Effekt des Schwellenwertparameters
- Der Schwellenwertparameter gibt eine Verschiebung der Verteilung weg vom Nullpunkt an. Ein negativer Schwellenwert verschiebt die Verteilung nach links, und ein positiver Schwellenwert verschiebt die Verteilung nach rechts. Alle Daten müssen größer als der Schwellenwert sein. Die Weibull-Verteilung mit 2 Parametern entspricht einer Weibull-Verteilung mit 3 Parametern, aber mit einem Schwellenwert von 0. Die Weibull-Verteilung (3;100;50) mit 3 Parametern weist beispielsweise die gleiche Form und Streubreite wie die Weibull-Verteilung (3;100) mit 2 Parametern auf, ist jedoch um 50 Einheiten nach rechts verschoben.