y-Skalentyp

Standardmäßig stellt die y-Skala eines Histogramms die Häufigkeit dar (jeder Balken entspricht der Häufigkeit von Werten innerhalb der angegebenen Einteilung), wobei der Betrag der einzelnen Einteilungen betont wird. Wenn die Zielgruppe nicht über ausreichende Fachkenntnisse in Bezug auf den dargestellten Prozess verfügt, um die Häufigkeitswerte interpretieren zu können, lässt sich der Typ der y-Skala in der Grafik ändern, um diese Häufigkeitswerte als Prozentwerte anzuzeigen (jeder Balken entspricht dem Prozentsatz aller Werte in der angegebenen Einteilung); möglicherweise ist dieses Format besser verständlich.

Standardmäßig stellt jeder Balken die Häufigkeit der Werte innerhalb der Einteilung dar. Ändern Sie den y-Skalentyp in Prozent, damit jeder Balken den Prozentsatz aller Werte innerhalb der Einteilung darstellt. Verwenden Sie Dichte, wenn Sie Verteilungen vergleichen möchten und die Stichproben unterschiedliche Umfänge aufweisen. Dichte ist auch hilfreich, wenn Sie Balken vergleichen möchten und die Einteilungsbreiten ungleich sind. Die Dichte wird als Anteil der Beobachtungen geteilt durch die Einteilungsbreite berechnet.

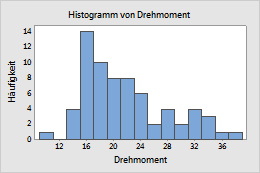
Häufigkeit (Standardeinstellung)

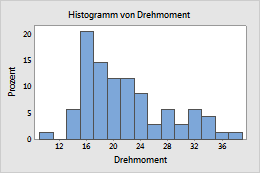
Prozent

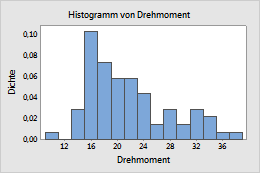
Dichte

Häufigkeit

Die Höhe jedes Balkens stellt die Anzahl der Beobachtungen in der Einteilung dar.

Prozent

Die Höhe jedes Balkens stellt den Prozentsatz der Stichprobenbeobachtungen in der Einteilung dar. Ein Histogramm mit einer Skala von Prozentsätzen wird gelegentlich auch als Histogramm der relativen Häufigkeiten bezeichnet. Verwenden Sie eine Skala von Prozentsätzen, um Stichproben mit unterschiedlichen Stichprobenumfängen zu vergleichen.

Dichte

Die Fläche jedes Balkens stellt den Anteil der Stichprobenbeobachtungen in der Einteilung dar (Anteil = Fläche des Balkens = Breite der Einteilung × Höhe des Balkens).

Werte einteilungsübergreifend kumulieren: (Nur Häufigkeiten- und Prozentskalen) Die Höhen der Balken werden von links nach rechts kumuliert. Die Höhe jedes Balkens entspricht der Summe aus der Höhe der Einteilung und allen vorhergehenden Einteilungen.

Prozent

Die Werte auf der y-Achse stellen die geschätzten kumulativen Prozentsätze dar. Der geschätzte kumulative Prozentsatz ist gleich dem Produkt aus der geschätzten kumulativen Wahrscheinlichkeit und 100.

Wahrscheinlichkeit

Die Werte auf der y-Achse stellen die geschätzten kumulativen Wahrscheinlichkeiten dar. Die kumulative Wahrscheinlichkeit für einen Wert x ist die Wahrscheinlichkeit, dass eine zufällige aus der Grundgesamtheit gewählte Beobachtung kleiner oder gleich x ist.

Minitab verwendet die Median-Rang-Methode (die auch als Benard-Methode bezeichnet wird), um die kumulative Wahrscheinlichkeit (r) für jede Beobachtung zu schätzen:

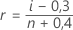
In dieser Formel ist i der Rang der Beobachtung in der Stichprobe, und n ist die Gesamtzahl der Beobachtungen in der Stichprobe. Für den kleinsten Wert in der Stichprobe ist i = 1, für den größten Wert in der Stichprobe i = n.

Wert (Nur Wahrscheinlichkeitsnetz)

Die Werte auf der y-Achse stellen die inversen kumulativen Wahrscheinlichkeiten dar.

Die Werte für die Normalverteilung und die lognormale Verteilung sind die inverse kumulative Wahrscheinlichkeit von r, die anhand der Standardnormalverteilung berechnet wird.

Die Werte für die Exponentialverteilung und die Weibull-Verteilung werden mit LN(–LN(1–r)) berechnet, wobei LN der natürliche Logarithmus ist.

Ähnlichkeit (Standardeinstellung)

Die Höhe jedes Clusters stellt die Ähnlichkeit dar. Die Ähnlichkeit s(ij) zwischen zwei Clustern i und j wird durch s(ij) = 100 (1 – d(ij) / d(max) angegeben. Wenn Sie für die Analyse die ursprüngliche Distanzmatrix D eingegeben haben, ist d(max) das Maximum in D. Falls D aus den Daten berechnet wurde, ist d(max) = 2, wenn Sie die Korrelation als Distanzmaß ausgewählt haben, und 1, wenn Sie die absolute Korrelation als Distanzmaß ausgewählt haben.

Distanz

Die Höhe jedes Clusters stellt die Distanz dar.